귀퉁이 서재
머신러닝 - 20. 특이값 분해(SVD) 본문

이번 장에서는 특이값 분해(SVD)에 대해 알아보겠습니다. 고유값 분해에 대해 알고 있어야 특이값 분해를 이해할 수 있습니다. 고유값 분해를 잘 모르시는 분은 이전 장을 참고해주시기 바랍니다. 이번 장은 MIT Open Course Ware, 파이썬 머신러닝 완벽 가이드 (권철민 저), 다크 프로그래머스 블로그를 참고했습니다.
특이값 분해(Singular Value Decomposition, SVD)
이전 장에서 고유값 분해에 대해 알아봤습니다. 고유값 분해는 정방 행렬(행과 열의 크기가 같은 행렬)에 대해서만 가능하다고 했습니다. 하지만 특이값 분해는 정방 행렬뿐만 아니라 행과 열의 크기가 다른 행렬에 대해서도 적용할 수 있습니다. 즉, 특이값 분해는 모든 직각 행렬에 대해 가능합니다.
SVD는 m x n 크기의 행렬 A를 다음과 같이 분해하는 것을 의미합니다.
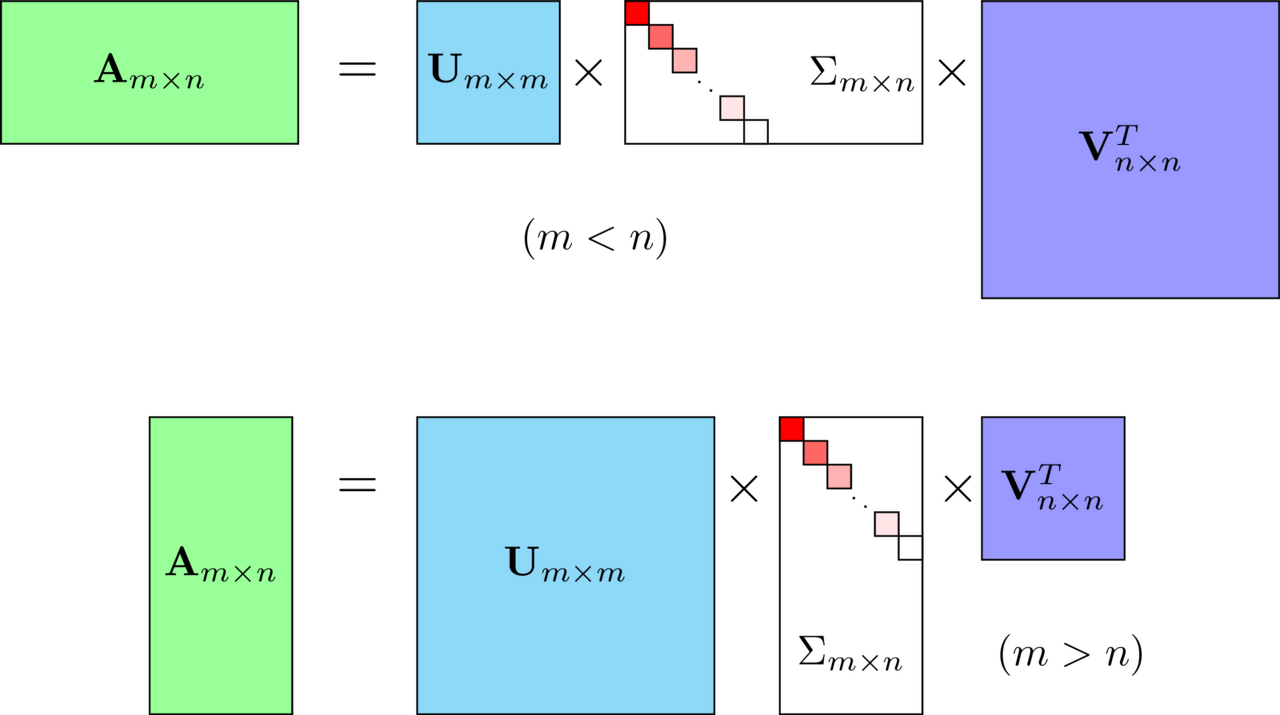
m x n 크기의 행렬 A는 m x m 크기의 행렬 U와 m x n 크기의 ∑ 그리고 n x n 크기의 Vt로 나뉩니다. (위 식에서 행렬 V의 전치 행렬(Transpose)은 편의상 Vt라 표기하겠습니다.)
행렬 U와 V에 속한 벡터를 특이 벡터(Singular Vector)라 합니다. 모든 특이 벡터는 서로 직교하는 성질을 가집니다. ∑는 직사각 대각 행렬이며, 행렬의 대각에 위치한 값만 0이 아니고 나머지 위치의 값은 모두 0입니다. m < n인 경우 첫번째와 같이 분해되며, m > n인 경우 두번째와 같이 분해됩니다. ∑의 0이 아닌 대각 원소값을 특이값(Singular Value)라고 합니다.
A = U ∑ Vt 를 하나하나 살펴보면 아래와 같습니다.

U는 AAt를 고유값 분해해서 얻은 직교 행렬이며, V는 AtA를 고유값 분해해서 얻은 직교 행렬입니다. 여기서 U와 V는 모두 직교 행렬입니다.
(※ 직교 행렬에 대해서는 이전 장에서 다뤘으니 자세한 사항은 이전 장을 참고해주시기 바랍니다. 행렬 U와 U의 전치 행렬 Ut를 내적했을 때 단위행렬 I가 되는 행렬을 직교 행렬이라고 합니다. U Ut = V Vt = I입니다. 행렬 U와 U의 역행렬을 내적해도 단위행렬 I가 되므로 Ut는 U의 역행렬과 같다는 특징이 있습니다.)
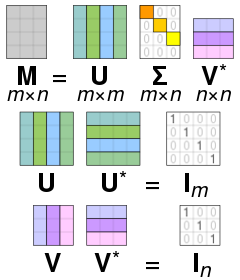
이때 U와 V에 속한 열 벡터를 특이 벡터(Singular Vector)라 한다고 했습니다. 특히 U에 속한 벡터를 Left Singular Vector, V에 속한 벡터를 Right Singular Vector라고 합니다. ∑는 m x n의 직사각 대각 행렬입니다. 대각 행렬의 대각 성분은 AtA 혹은 AAt의 고유값들에 루트를 씌워준 값으로 구성되어 있습니다.
대칭 행렬은 모두 고유값 분해가 가능하며, 더군다나 직교 행렬로 분해할 수 있습니다. AAt와 AtA는 모두 대칭 행렬이므로 고유값 분해가 가능합니다. AAt = U (∑ ∑t) Ut 로 분해할 수 있습니다. (증명은 아래 사진 참고) 다시 말해 (∑ ∑t)의 대각 원소 값은 AAt의 고유값(eigen value)이며, U는 AAt의 고유 벡터들로 구성된 행렬입니다. 마찬가지로 V는 AtA를 고유값 분해해서 얻은 행렬입니다. (∑t ∑)의 대각 원소 값은 AtA의 고유값(eigen value)이며, V는 AtA의 고유 벡터들로 구성된 행렬입니다.

다시 정리해보겠습니다. SVD는 특이값 분해라고 하며, 행렬 U와 V에 속한 벡터를 특이 벡터(Singular Vector)라 합니다. 모든 특이 벡터는 서로 직교하는 성질을 가집니다. ∑는 대각행렬이며, 행렬의 대각에 위치한 값만 0이 아니고 나머지 위치의 값은 모두 0입니다. ∑의 대각 원소 값이 바로 행렬 A의 특이값(Singular Value)입니다. A의 특이값은 AAt 혹은 AtA의 고유값의 루트(Square Root) 값과 같습니다. (여기서 AAt이 고유값과 AtA의 고유값이 같습니다. AAt의 고유값과 AtA의 고유값이 왜 같은지는 다크 프로그래머스 블로그에서 증명해놨습니다. 궁금하신 분들은 다크 프로그래머스 블로그를 참고해주시기 바랍니다.)
특이값 분해(SVD)의 기하학적 의미
이전 장에서 설명드렸듯이 모든 행렬은 선형 변환을 뜻합니다. 직교 행렬은 선형 변환 중 회전 변환을 의미합니다. 또한, 대각 행렬은 스케일 변환을 의미합니다.
A = U ∑ Vt에서 행렬 A의 선형 변환을 해보겠습니다. 먼저 Vt로 회전 변환(Rotate)을 하고 ∑로 스케일 변환(Stretch)를 한 뒤 다시 U로 회전 변환(Rotate)을 하는 걸 볼 수 있습니다. 기하학적으로 표현하자면 아래와 같습니다.
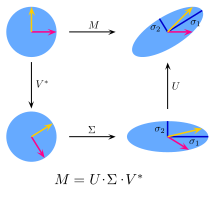
따라서 행렬의 특이값(Singular Value)은 이 행렬로 표현되는 선형 변환의 스케일 변환(Stretch)을 나타내는 값입니다.
SVD의 기하학적 의미를 조금 더 직관적인 질문을 통해 이해해보겠습니다.
"직교하는 벡터 집합 V = (v₁, v₂, ...)에 대하여 선형 변환 후에도 그 크기는 변하지만 여전히 직교하게 만드는 그 직교 벡터 집합은 무엇이고, 변경 후의 벡터 집합은 무엇인가?"라는 질문을 보시죠.
A = U ∑ Vt 에서 양변에 V를 내적해주면, A V = U ∑ 가 됩니다. U와 V에 속한 벡터는 서로 직교하는 성질을 가진다고 했습니다. 따라서 서로 직교하는 벡터로 구성된 행렬 V에 선형 변환 A를 해준 뒤에도 서로 직교하는 벡터로 구성된 행렬 U가 만들어집니다. 다만 그 크기가 ∑만큼 차이가 있습니다.
직교하는 벡터 집합 V에 대하여 선형 변환 A 후에도 그 크기는 ∑만큼 변하지만 여전히 직교하는 벡터 집합 U를 만듭니다.
특이값 분해를 처음 접하면 이해하기가 쉽지 않습니다. ㅜㅜ 블로그 하단에 링크를 걸어둔 Reference를 참고해주시면 이해가 수월할 수 있습니다. reference4 -> reference1 -> reference2 순으로 보시기 바랍니다.
Full SVD와 Truncated SVD
행렬 A를 m x m 크기인 U, m x n 크기인 ∑, n x n 크기인 Vt 로 특이값 분해(SVD)하는 것을 Full SVD라고 합니다.
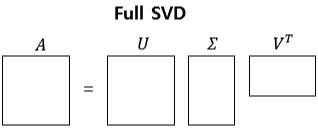
하지만 Full SVD를 사용하는 경우는 드뭅니다. 실제로는 ∑의 비대각 부분과 대각 원소 중 특이값이 0인 부분을 모두 제거하고, 제거된 ∑에 대응되는 U와 V 원소도 함께 제거해 차원을 줄인 형태로 SVD를 적용합니다. 이런 방식을 Truncated SVD라고 합니다. 다시 말해 Truncated SVD는 ∑의 대각 원소 중 상위 몇 개만 추출하고 여기에 대응하는 U와 V의 원소도 함께 제거해 차원을 줄인 것입니다. ∑의 대각 원소 중 상위 t개만 추출한다고 하면 아래와 같이 분해됩니다.

Ut의 크기는 m x t이며, ∑t의 크기는 t x t, 그리고 Transpose of Vt의 크기는 t x n입니다. (여기서 ∑t, Vt에서 t의 의미는 전치 행렬을 뜻하는 transpose가 아니라 Truncated SVD에서 상위 t개만 추출한다는 의미의 t입니다) 그리고 Truncated SVD로 한번 분해를 하면 원본 행렬인 A로 원복할 수 없습니다. Full SVD는 분해를 해도 모든 원소가 남아있기 때문에 원본 행렬 A로 원복이 가능하지만 Truncated SVD는 원소를 손실하기 때문에 원복이 불가합니다. 하지만 근사하게는 일치합니다. t가 클수록 원래의 행렬 A와 가까워지며, t가 작아질수록 원본 행렬 A와 차이가 많이 납니다.
특이값 분해(SVD) 및 원본 행렬 복원 실습
# numpy의 svd 모듈 import
import numpy as np
from numpy.linalg import svd
# 4X4 Random 행렬 a 생성
np.random.seed(121)
a = np.random.randn(4,4)
print(np.round(a, 3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]4 x 4 크기의 행렬 a를 만들었습니다. 이제 Full SVD를 해보겠습니다. Full SVD는 numpy에서도 지원이 됩니다.
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape)
print('U matrix:\n',np.round(U, 3))
print('Sigma Value:\n',np.round(Sigma, 3))
print('V transpose matrix:\n',np.round(Vt, 3))(4, 4) (4,) (4, 4)
U matrix:
[[-0.079 -0.318 0.867 0.376]
[ 0.383 0.787 0.12 0.469]
[ 0.656 0.022 0.357 -0.664]
[ 0.645 -0.529 -0.328 0.444]]
Sigma Value:
[3.423 2.023 0.463 0.079]
V transpose matrix:
[[ 0.041 0.224 0.786 -0.574]
[-0.2 0.562 0.37 0.712]
[-0.778 0.395 -0.333 -0.357]
[-0.593 -0.692 0.366 0.189]]생성한 행렬 a에 SVD를 해주면 U 행렬, Sigma 행렬, V의 전치 행렬을 반환합니다. Sigma행렬의 경우 대각에 위치한 값만 0이 아니고, 나머지 값은 모두 0이므로 0이 아닌 값만 1차원 행렬로 반환합니다. 이 값들이 바로 행렬 a의 특이값(Singular Value)입니다.
분해된 U, Sigma, Vt를 이용해 원본 행렬로 복원해보겠습니다. 원복을 위해서는 U, Sigma, Vt를 내적하면 됩니다. 한 가지 주의할 점은 Sigma는 1차원 행렬이므로 다시 0을 포함한 대각 행렬로 변환한 뒤 내적을 수행해줘야 한다는 점입니다.
# Sima를 다시 0 을 포함한 대칭행렬로 변환
Sigma_mat = np.diag(Sigma)
a_ = np.dot(np.dot(U, Sigma_mat), Vt)
print(np.round(a_, 3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]결과는 원본 행렬과 동일합니다. Full SVD로 분해한 U, Sigma, Vt를 내적하면 원본 행렬과 정확히 일치함을 알 수 있습니다.
이번에는 Truncated SVD를 이용해 행렬을 분해해보겠습니다. 앞서 설명한 바와 같이 Truncated SVD는 ∑ 행렬에 있는 상위 일부 원소만 추출해 분해하는 방식입니다. 이렇게 분해하면 인위적으로 더 작은 차원의 U, ∑, Vt 로 분해하기 때문에 데이터가 소실되어 원본 행렬을 정확하게 다시 원복할 수 없습니다. Truncated SVD는 numpy가 아닌 scipy에서만 지원합니다.
import numpy as np
from scipy.sparse.linalg import svds
from scipy.linalg import svd
# 원본 행렬을 출력하고, SVD를 적용할 경우 U, Sigma, Vt 의 차원 확인
np.random.seed(121)
matrix = np.random.random((6, 6))
print('원본 행렬:\n',matrix)
U, Sigma, Vt = svd(matrix, full_matrices=False)
print('\n분해 행렬 차원:',U.shape, Sigma.shape, Vt.shape)
print('\nSigma값 행렬:', Sigma)
# Truncated SVD로 Sigma 행렬의 특이값을 4개로 하여 Truncated SVD 수행.
num_components = 4
U_tr, Sigma_tr, Vt_tr = svds(matrix, k=num_components)
print('\nTruncated SVD 분해 행렬 차원:',U_tr.shape, Sigma_tr.shape, Vt_tr.shape)
print('\nTruncated SVD Sigma값 행렬:', Sigma_tr)
matrix_tr = np.dot(np.dot(U_tr,np.diag(Sigma_tr)), Vt_tr) # output of TruncatedSVD
print('\nTruncated SVD로 분해 후 복원 행렬:\n', matrix_tr)원본 행렬:
[[0.11133083 0.21076757 0.23296249 0.15194456 0.83017814 0.40791941]
[0.5557906 0.74552394 0.24849976 0.9686594 0.95268418 0.48984885]
[0.01829731 0.85760612 0.40493829 0.62247394 0.29537149 0.92958852]
[0.4056155 0.56730065 0.24575605 0.22573721 0.03827786 0.58098021]
[0.82925331 0.77326256 0.94693849 0.73632338 0.67328275 0.74517176]
[0.51161442 0.46920965 0.6439515 0.82081228 0.14548493 0.01806415]]
분해 행렬 차원: (6, 6) (6,) (6, 6)
Sigma값 행렬: [3.2535007 0.88116505 0.83865238 0.55463089 0.35834824 0.0349925 ]
Truncated SVD 분해 행렬 차원: (6, 4) (4,) (4, 6)
Truncated SVD Sigma값 행렬: [0.55463089 0.83865238 0.88116505 3.2535007 ]
Truncated SVD로 분해 후 복원 행렬:
[[0.19222941 0.21792946 0.15951023 0.14084013 0.81641405 0.42533093]
[0.44874275 0.72204422 0.34594106 0.99148577 0.96866325 0.4754868 ]
[0.12656662 0.88860729 0.30625735 0.59517439 0.28036734 0.93961948]
[0.23989012 0.51026588 0.39697353 0.27308905 0.05971563 0.57156395]
[0.83806144 0.78847467 0.93868685 0.72673231 0.6740867 0.73812389]
[0.59726589 0.47953891 0.56613544 0.80746028 0.13135039 0.03479656]]크기가 6 x 6인 행렬을 Full SVD 분해하면 U, Sigma, Vt가 각각 (6 ,6), (6,), (6, 6)의 크기를 갖지만, 추출하고자 하는 대각 원소의 개수를 4로 설정한 Truncated SVD 분해를 하면 U, Sigma, Vt는 각각 (6, 4), (4,), (4, 6)의 크기를 갖습니다. 또한 Truncated SVD의 경우 U, Sigma, Vt를 내적 했을 때 원본 행렬과 정확하게 일치하지 않고 근사적으로 복원되는 것을 볼 수 있습니다.
지금까지 SVD에 대해 알아봤습니다. SVD는 매우 많은 피처를 가진 고차원 행렬을 저차원 행렬로 분리하는 행렬 분해 기법입니다. 특히 이런 행렬 분해를 수행하면서 원본 행렬에서 잠재된 요소를 추출하기 때문에 토픽 모델링이나 추천 시스템에 활발하게 사용됩니다.
references
reference1: MIT OpenCourseWare (Singular Value Decomposition)
reference2: 다크 프로그래머스 (특이값 분해의 활용)
reference3: 파이썬 머신러닝 완벽 가이드 (권철민 저)
reference4: 공돌이의 수학정리노트 유튜브 (특이값 분해의 기하학적 의미와 활용 소개)
'머신러닝' 카테고리의 다른 글
| 《머신러닝·딥러닝 문제해결 전략》책을 출간했습니다. (10) | 2022.04.24 |
|---|---|
| 머신러닝 - 19. 고유값(eigenvalue), 고유벡터(eigenvector), 고유값 분해(eigen decomposition) (2) | 2020.02.24 |
| 머신러닝 - 18. 선형판별분석(LDA) (0) | 2020.01.01 |
| 머신러닝 - 17. 회귀 평가 지표 (8) | 2019.12.06 |
| 머신러닝 - 16. NGBoost (16) | 2019.11.01 |




