귀퉁이 서재
NLP - 8. 코사인 유사도(Cosine Similarity) 본문

문서 유사도란 말그대로 문서와 문서 간의 유사도가 어느정도인지 나타내는 척도입니다. 문서 간 유사도를 측정해 지금 보고 있는 뉴스와 가장 유사한 뉴스를 추천해주기도 하고, 줄거리를 기반으로 내가 본 영화와 가장 유사한 영화를 추천해줄 수도 있습니다. 문서 유사도를 측정하는 방법은 여러개가 있지만 일반적으로 코사인 유사도(Cosine Similarity)를 많이 사용합니다. 이번 장에서는 코사인 유사도의 정의와 사용 방법에 대해 알아보겠습니다. 역시나 이전과 마찬가지로 파이썬 머신러닝 완벽 가이드 (권철민 저), 딥 러닝을 이용한 자연어 처리 입문 (유원주 저)을 요약정리했습니다.
코사인 유사도 (Cosine Similarity)
코사인 유사도란 벡터와 벡터 간의 유사도를 비교할 때 두 벡터 간의 사잇각을 구해서 얼마나 유사한지 수치로 나타낸 것입니다. 벡터 방향이 비슷할수록 두 벡터는 서로 유사하며, 벡터 방향이 90도 일때는 두 벡터 간의 관련성이 없으며, 벡터 방향이 반대가 될수록 두 벡터는 반대 관계를 보입니다.
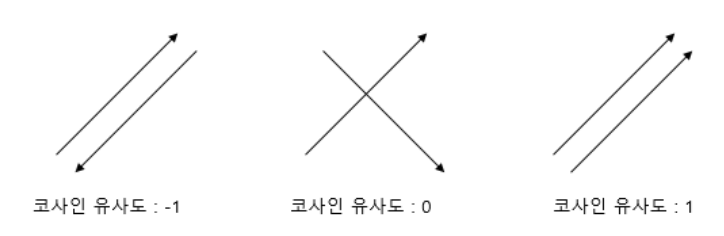
코사인 유사도는 두 벡터 간의 사잇각을 코사인 씌워준 값을 통해 구해줄 수 있습니다. 중학교 때 배웠던 코사인 함수를 상기해봅시다.
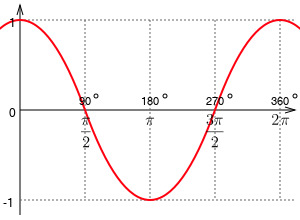
θ를 두 벡터 간의 사잇각이라고 했을 때 θ=0이면, cosθ = 1입니다. 코사인 유사도가 1이면 두 벡터는 완전히 동일한 벡터입니다. 마찬가지로 두 벡터 간의 사잇각이 90도이면, 코사인 유사도가 0이되고 두 벡터는 상관 관계가 없다고 말합니다. 두 벡터 간의 사잇각이 180도 이면 코사인 유사도는 -1이며, 두 벡터는 완전히 반대인 벡터입니다.
하지만 피처 벡터 행렬은 음수값이 없으므로 코사인 유사도가 음수가 되지는 않습니다. 따라서 코사인 유사도는 0~1 사이의 값을 갖습니다.
다시 중학교 수학을 상기해봅시다. 벡터의 내적은 각 벡터의 절대 값에 코사인을 곱한 것입니다.

그러면 cosθ = A º B / |A| * |B| 입니다. 따라서 코사인 유사도를 구하는 식은 아래와 같습니다. (즉, 내적의 결과를 총 벡터 크기로 정규화(L2 Normalization)한 것입니다.)
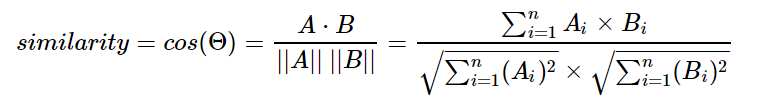
문서 간 유사도를 측정하는 방법 중 유클리드 거리 기반의 지표도 있습니다. 하지만 희소 행렬에서 문서와 문서 벡터 간의 크기에 기반한 유사도 지표는 정확도가 떨어집니다. 또한 문서가 매우 긴 경우 단어의 빈도수 또한 많기 때문에 빈도수에만 기반해서 유사도를 구하는 것은 공정한 비교가 될 수 없습니다. 예를 들어 A 문서에서 '경제'라는 단어가 5번 나왔고, B 문서에서 '경제'라는 단어가 3번 언급되었다고 A가 경제와 더 밀접한 문서라고 볼 수 없습니다. A 문서의 길이가 B 문서의 길이보다 10배 이상 크다면 오히려 B 문서가 경제와 더 관련이 있다고 판단해야 옳을 것입니다. 따라서 문서 간 유사도를 측정할 때는 코사인 유사도가 가장 많이 쓰입니다.
문장 간 코사인 유사도 구하기
문서 간의 코사인 유사도를 구하는 실습을 해보겠습니다. 우선, 코사인 유사도를 구하는 함수를 생성합니다.
import numpy as np
def cos_similarity(v1, v2):
dot_product = np.dot(v1, v2)
l2_norm = (np.sqrt(sum(np.square(v1))) * np.sqrt(sum(np.square(v2))))
similarity = dot_product / l2_norm
return similarity코사인 유사도를 구하기 위해, 문서를 TF-IDF 벡터화된 행렬로 변환합니다.
from sklearn.feature_extraction.text import TfidfVectorizer
doc_list = ['if you take the blue pill, the story ends' ,
'if you take the red pill, you stay in Wonderland',
'if you take the red pill, I show you how deep the rabbit hole goes']
tfidf_vect_simple = TfidfVectorizer()
feature_vect_simple = tfidf_vect_simple.fit_transform(doc_list)
print(feature_vect_simple.shape)
print(type(feature_vect_simple))(3, 18)
<class 'scipy.sparse.csr.csr_matrix'>문서가 3개, 총 단어의 갯수(중복 제거)가 18개이므로 TF-IDF 벡터화 한 행렬은 3 X 18 행렬입니다. 또한, 변환된 행렬은 희소 행렬이므로 앞에서 작성한 cos_similarity( ) 함수의 인자인 arrary로 만들기 위해 밀집 행렬로 변환하고, 다시 배열로 변환해야 합니다.
# TFidfVectorizer로 transform()한 결과는 Sparse Matrix이므로 Dense Matrix로 변환.
feature_vect_dense = feature_vect_simple.todense()
#첫번째 문장과 두번째 문장의 feature vector 추출
vect1 = np.array(feature_vect_dense[0]).reshape(-1,)
vect2 = np.array(feature_vect_dense[1]).reshape(-1,)
#첫번째 문장과 두번째 문장의 feature vector로 두개 문장의 Cosine 유사도 추출
similarity_simple = cos_similarity(vect1, vect2)
print('문장 1, 문장 2 Cosine 유사도: {0:.3f}'.format(similarity_simple))문장 1, 문장 2 Cosine 유사도: 0.402feature_vect_simple.todense()는 희소 행렬인 feature_vect_simple을 밀집 행렬로 변환하는 코드입니다. 첫번째 문장과 두번째 문장의 코사인 유사도는 0.402입니다.
사이킷런은 코사인 유사도를 측정하기 위한 cosine_similarity() API를 제공합니다. 이 API를 사용하면 위와 같이 일일이 계산하지 않아도 쉽게 코사인 유사도를 구할 수 있습니다. cosine_similarity() 함수의 첫번째 인자는 비교 기준이 되는 문서의 피처 행렬, 두번째 인자는 비교하고자 하는 문서의 피처 행렬이 들어가면 됩니다. 그리고 희소 행렬, 밀집 행렬이 모두 가능하며, 행렬과 배열 모두 가능합니다. 첫번째 문장과 나머지 문장의 코사인 유사도를 측정해보겠습니다.
from sklearn.metrics.pairwise import cosine_similarity
similarity_simple_pair = cosine_similarity(feature_vect_simple[0] , feature_vect_simple)
print(similarity_simple_pair)[[1. 0.40207758 0.40425045]]아래와 같이 코사인 유사도를 행렬로 표현할 수도 있습니다.
similarity_simple_pair = cosine_similarity(feature_vect_simple , feature_vect_simple)
print(similarity_simple_pair)[[1. 0.40207758 0.40425045]
[0.40207758 1. 0.45647296]
[0.40425045 0.45647296 1. ]]지금까지 문서 간의 유사도를 측정할 수 있는 코사인 유사도에 대해 알아봤습니다.
References
Reference1: 파이썬 머신러닝 완벽 가이드 (권철민 저)
'자연어 처리 (NLP)' 카테고리의 다른 글
| NLP - 10. 워드 임베딩 (Word Embedding) (2) | 2020.06.14 |
|---|---|
| NLP - 9. 토픽 모델링: 잠재 의미 분석(LSA) (0) | 2020.03.19 |
| NLP - 7. 희소 행렬 (Sparse Matrix) - COO 형식, CSR 형식 (6) | 2020.02.16 |
| NLP - 6. 카운트 기반 벡터화(CountVectorizer)와 TF-IDF 벡터화 (2) | 2020.02.15 |
| NLP - 5. Bag of Words (BOW) (0) | 2020.02.13 |




