귀퉁이 서재
머신러닝 - 18. 선형판별분석(LDA) 본문

선형판별분석(Linear Discriminant Analysis, LDA)
선형판별분석(Linear Discriminant Analysis, LDA)는 PCA와 마찬가지로 축소 방법 중 하나입니다. (구글에 LDA라고 치면 토픽 모델링 기법인 Latent Dirichlet Allocation이 주로 나올 겁니다. 이와는 다른 개념인 선형판별분석에 대한 글입니다.) LDA는 PCA와 유사하게 입력 데이터 세트를 저차원 공간으로 투영(project)해 차원을 축소하는 기법이지만, PCA와 다르게 LDA는 지도학습의 분류(Classification)에서 사용됩니다.
LDA 원리
PCA는 데이터의 변동성이 최대가 되는 축을 찾아 주성분으로 정했지만, LDA는 데이터의 Target값 클래스끼리 최대한 분리할 수 있는 축을 찾습니다. 아래 그림을 통해 설명해보겠습니다.
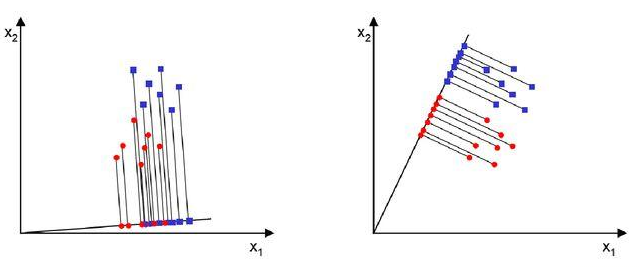
파란색 점과 빨간색 점을 서로 분류한다고 했을 때 왼쪽 축과 오른쪽 축 가운데 어떤 것이 더 분류가 잘 되었다고 판단할 수 있을까요? 오른쪽 축입니다. 왼쪽의 데이터들을 축으로 투영(project)했을 때 빨간색과 파란색이 서로 겹치는 부분이 많습니다. 반면, 오른쪽 데이터들을 축으로 사영했을 때 빨간색과 파란색이 명확히 분류가 되었습니다.
LDA는 바로 오른쪽과 같이 분류를 해주는 기법입니다. 투영 후 두 클래스 간 분산은 최대한 크게 가져가고, 클래스 내부의 분산은 최대한 작게 가져가는 방식입니다. 클래스 간 분산이 최대가 된다는 것은 각 클래스의 중심(평균)이 서로 멀어지도록 분류한다는 것입니다. 클래스 내부의 분산이 작아진다는 것은 하나의 클래스끼리는 오밀조밀하게 뭉쳐있다는 뜻입니다. 클래스 간 분산이 최대가 되고 클래스 내부 분산이 최소가 되면 [(클래스 간 분산) / (클래스 내부 분산)]은 최대가 됩니다.
다시 말하자면 LDA는 특정 공간상에서 클래스 분리를 최대화하는 축을 찾기 위해 클래스 간 분산(between-class scatter)과 클래스 내부 분산(within-class scatter)의 비율을 최대화하는 방식으로 차원을 축소합니다.
LDA은 투영을 통해 가능한 한 클래스를 멀리 떨어지게 하므로 SVM 같은 다른 분류 알고리즘을 적용하기 전에 차원을 축소시키는 데 사용하면 좋습니다.
붓꽃 데이터 세트를 활용한 LDA 실습
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# 붓꽃 데이터 로드
iris = load_iris()
# 데이터 정규 스케일링
iris_scaled = StandardScaler().fit_transform(iris.data)
# 2개의 클래스로 구분하기 위한 LDA 생성
lda = LinearDiscriminantAnalysis(n_components=2)
# fit()호출 시 target값 입력
lda.fit(iris_scaled, iris.target)
iris_lda = lda.transform(iris_scaled)
lda_columns=['lda_component_1','lda_component_2']
irisDF_lda = pd.DataFrame(iris_lda, columns=lda_columns)
irisDF_lda['target']=iris.target
#setosa는 세모, versicolor는 네모, virginica는 동그라미로 표현
markers=['^', 's', 'o']
#setosa의 target 값은 0, versicolor는 1, virginica는 2. 각 target 별로 다른 shape으로 scatter plot
for i, marker in enumerate(markers):
x_axis_data = irisDF_lda[irisDF_lda['target']==i]['lda_component_1']
y_axis_data = irisDF_lda[irisDF_lda['target']==i]['lda_component_2']
plt.scatter(x_axis_data, y_axis_data, marker=marker,label=iris.target_names[i])
plt.legend(loc='upper right')
plt.xlabel('lda_component_1')
plt.ylabel('lda_component_2')
plt.show()
붓꽃 데이터는 setosa, versicolor, virginica로 3종류이지만 위 코드에서는 편의상 2개의 클래스로 분류했습니다. setosa가 하나의 클래스, versicolor, virginica의 합이 또 다른 클래스로 분류되었습니다. 주의할 점은 LDA는 PCA와 다르게 지도학습 분류이므로 fit할 때, target값을 입력해주어야 합니다. iris_scaled는 feature 데이터, iris.target은 target 데이터입니다.
lda.fit(iris_scaled, iris.target)References
Reference1: 파이썬 머신러닝 완벽가이드 (권철민 저)
Reference2: 핸즈온 머신러닝 (오렐리앙 제롱 저)
'머신러닝' 카테고리의 다른 글
| 머신러닝 - 20. 특이값 분해(SVD) (0) | 2020.03.01 |
|---|---|
| 머신러닝 - 19. 고유값(eigenvalue), 고유벡터(eigenvector), 고유값 분해(eigen decomposition) (4) | 2020.02.24 |
| 머신러닝 - 17. 회귀 평가 지표 (8) | 2019.12.06 |
| 머신러닝 - 16. NGBoost (16) | 2019.11.01 |
| 머신러닝 - 15. 그레디언트 부스트(Gradient Boost) (40) | 2019.10.23 |




