귀퉁이 서재
머신러닝 - 2. 서포트 벡터 머신 (SVM) 개념 본문

서포트 벡터 머신(SVM, Support Vector Machine)이란 주어진 데이터가 어느 카테고리에 속할지 판단하는 이진 선형 분류 모델입니다. (Reference1) 본 포스트는 Udacity의 SVM 챕터를 정리한 것입니다.
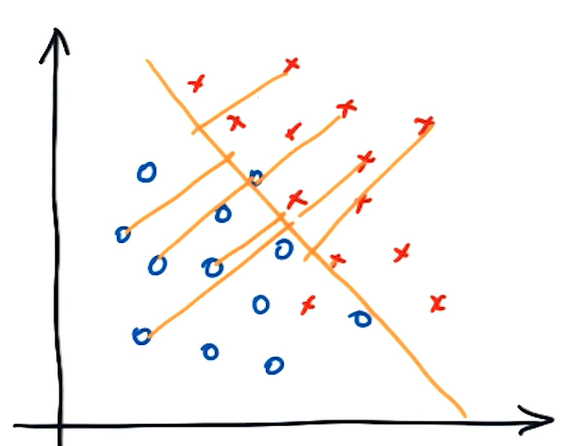
아래 그림을 봅시다. 빨간 X와 파란 O를 구분하는 3개의 선을 나타낸 것입니다. 3개 선 중 어떤 선이 가장 적절하게 두 데이터를 구분한 선일까요?

표시가 된 가운데 선이 가장 적절합니다. 왜 양 옆의 선보다 가운데 선이 두 데이터를 더 적절히 구분하는 선일까요?
Margin의 최대화
정답은 가운데 선이 Margin을 최대화하기 때문입니다. Margin이란 선과 가장 가까운 양 옆 데이터와의 거리입니다. 선과 가장 가까운 포인트를 서포트 벡터(Support vector)라고 합니다. 즉, Margin은 구분하는 선과 서포트 벡터와의 거리를 의미합니다. 또한 이렇게 두 데이터를 구분하는 선을 Decision Boundary라고 합니다. 본 포스트에서는 Decision Boundary를 편의상 구분선이라고 부르겠습니다. 이제 아래 그림을 보겠습니다.
Robustness

세 개의 선 중 어떤 것이 Margin을 최대화할까요? 바로 가운데 선입니다. 왼쪽 선은 파란 서포트 벡터와의 거리는 길지만 빨간 서포트 벡터와의 거리는 짧습니다. 반면 가운데 선은 빨간 서포트 벡터, 파란 서포트 벡터와의 거리가 같습니다. 각 서포트 벡터와의 Margin을 최대화하는 방향으로 구분선을 잡아야 하므로 가운데 선이 가장 적절한 구분 선이 됩니다. 이렇게 양 옆 서포트 벡터와의 Margin을 최대화하면 robustness도 최대화가 됩니다. 데이터 과학에서 로버스트(robust)하다는 말을 많이 씁니다. 로버스트하다는 것은 아웃라이어(outlier)의 영향을 받지 않는다는 뜻입니다. 아래 예시를 들어 설명해보겠습니다.
1, 2, 3, 4, 5 이렇게 총 5개 데이터가 있습니다. 이 데이터의 평균은 3입니다. 중앙값도 3입니다.
1, 2, 3, 4, 100으로 데이터가 바뀌었다고 합시다. 5가 100으로 바뀐 것입니다. 이제 평균은 22입니다. 중앙값은 여전히 3입니다. 평균은 100이라는 아웃라이어(outlier)의 영향을 받아서 크게 바뀌었고, 중앙값은 아웃라이어의 영향을 전혀 받지 않아 바뀌지 않았습니다. 이때 평균은 로버스트(robust)하지 않다고 하고, 중앙값은 로버스트(robust)하다고 합니다. 우리말로 강건하다는 뜻입니다.
자, 이제 다시 서포트 벡터로 돌아가 보겠습니다. 위 그림에서 왼쪽 선은 로버스트하지 않고, 가운데 선은 로버스트합니다. 만약 빨간색 포인트에 노이즈가 생겨 지금보다 더 오른쪽에 빨간 포인트가 찍힌다면 왼쪽 선은 빨간 포인트와 파란 포인트를 적절히 구분해주지 못합니다. 왼쪽 선 기준으로 오른쪽에 빨간 포인트가 찍혔다면 두 데이터를 제대로 구분 못 한 것이지요. 따라서 왼쪽 선은 로버스트하지 못합니다. 이렇듯 Margin을 최대화하면 robustness도 최대화가 됩니다.
데이터의 정확한 분류

둘 중 어떤 선이 SVM의 구분선으로 적절할까요? 표시가 된 아래 구분선입니다. 첫 번째 구분선이 Margin이 더 크긴합니다. 하지만 첫 번째 구분선은 데이터를 정확히 구분하지 못합니다. 구분선 아래 빨간 포인트가 있으니까요. SVM은 무작정 Margin을 크게 하는 구분선을 택하는 것이 아닙니다. 우선, 데이터를 정확히 분류하는 범위를 먼저 찾고, 그 범위 안에서 Margin을 최대화하는 구분선을 택하는 것입니다.
Outlier 처리
이번엔 아래 예제를 보겠습니다. 빨간 포인트 사이에 파란 포인트가 하나 섞여있습니다. 즉, outlier가 하나 있는 것입니다. 이때는 어떤 구분선이 적합할까요?

표시된 맨 오른쪽 구분선이 가장 적합합니다. 이전 예제처럼 SVM은 우선 두 데이터를 정확히 구분하는 선을 찾습니다. 하지만 두 데이터를 정확히 구분하는 직선은 없습니다. 이럴 땐 SVM이 어느 정도 outlier를 무시하고 최적의 구분선을 찾습니다. 위 예제에서 빨간 포인트 사이에 섞인 파란 포인트는 outlier로 취급해서 무시하고 Margin을 최대화하는 구분선을 찾은 것입니다.
커널 트릭 (Kernel Trick)
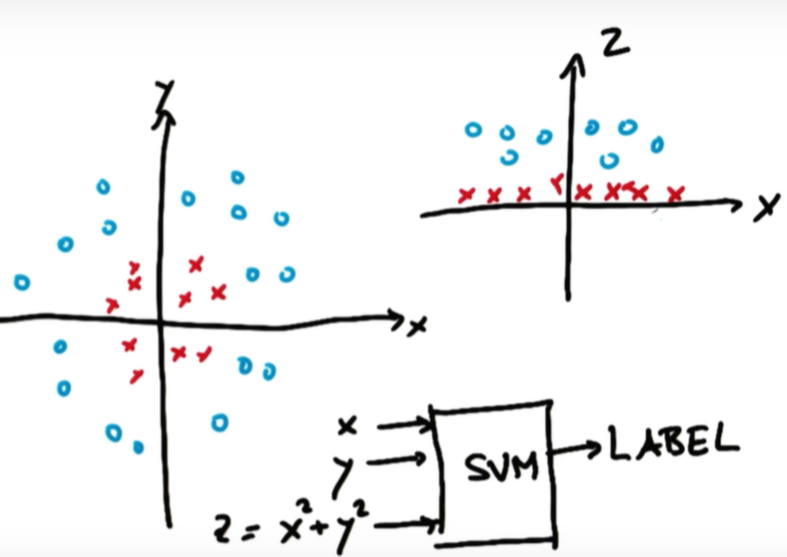
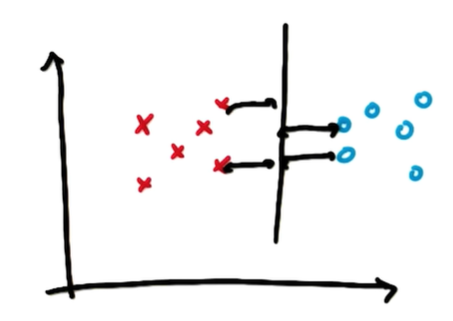
x와 y축으로 이루어진 왼쪽 좌표를 먼저 보겠습니다. 빨간 포인트와 파란 포인트를 구분할 수 있는 linear line은 없습니다. 아웃라이어를 무시하고 그릴 수 있는 상황도 아닙니다. 이럴 땐 어떻게 해야 할까요? 차원을 바꿔주어 구분선을 그릴 수 있습니다. z = x^2 + y^2라고 하고, 오른쪽처럼 z와 x로 이루어진 좌표를 그립니다. 그러면 왼쪽 그래프가 오른쪽 그래프처럼 바뀝니다. z는 원점으로부터 해당 데이터까지 떨어진 거리의 제곱과 같습니다. 따라서 빨간 포인트는 원점으로부터의 거리가 짧아 z가 작고, 파란 포인트는 원점으로부터의 거리가 길어 z가 큽니다. 왼쪽 그래프에서는 linear line을 그릴 수 없었는데, 오른쪽 그래프에서는 linear line으로 구분할 수 있습니다. 즉, 선형으로 분류할 수 있게 된 것입니다. (It can be linearly separable)
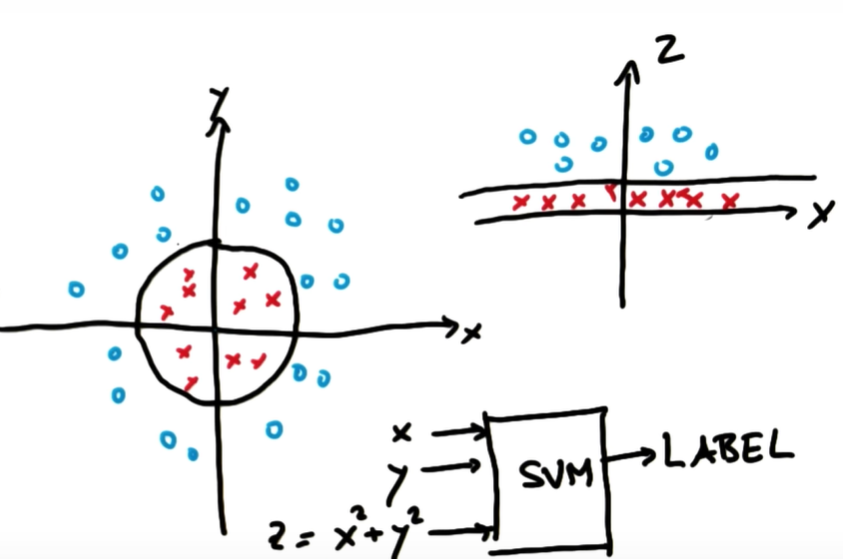
오른쪽 그래프에서 linear하게 그린 구분선은 왼쪽에서 원형으로 된 구분선과 동일합니다. 차원이 달라져서 구분선의 모양이 다른 것뿐입니다. x, y로만 이루어진 평면을 x, y, z 평면으로 차원 확대를 하니 구분선을 쉽게 그릴 수 있었습니다. 이렇듯 저차원 공간(low dimensional space)을 고차원 공간(high dimensional space)으로 매핑해주는 작업을 커널 트릭(Kernel Trick)이라고 합니다.
이를 입체적으로 보여주는 동영상 자료 (Reference2)를 참고해주시기 바랍니다. (40초가량)
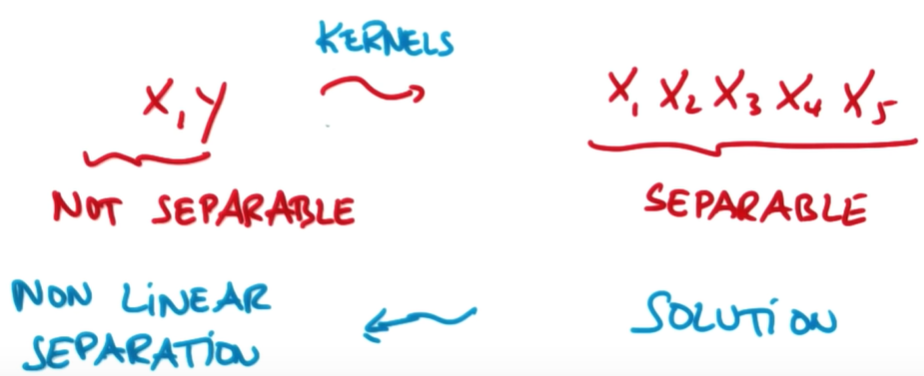
위 예제에서 x, y로 이루어진 저차원 공간(low dimensional space)은 linear separable하지 않습니다. 이를 커널 트릭(Kernel Trick)을 이용하여 고차원 공간(high dimensional space)으로 매핑합니다. 고차원 공간에서는 저차원 공간에서 보다 쉽게 linear separable line을 구할 수 있습니다. 이 line을 다시 저차원 공간으로 매핑하면 non linear separable line이 구해집니다. 처음부터 저차원 공간에서 non linear separable line을 구하려면 쉽지 않습니다. 따라서 커널 트릭을 활용하여 먼저 고차원 공간에서의 linear한 해를 구한 뒤 저차원 공간에서의 non linear한 해를 구한 것입니다. 이것은 머신러닝의 중요한 기법 중 하나입니다.
sklearn SVM Parameter
사이킷 런 SVM의 중요한 파라미터인 kernel, C, Gamma에 대해 설명해보겠습니다. (Reference3)
Kernel
sklearn에서 kernel parameter로 linear, polynomial, sigmoid, rbf 등의 kernel을 선택할 수 있습니다. (Reference4) default는 rbf입니다. 각 요소에 대한 설명은 Reference4를 참고해주시기 바랍니다.
다음 중 kernel = linear, gamma = 1.0인 SVM은 어떤 것일까요?
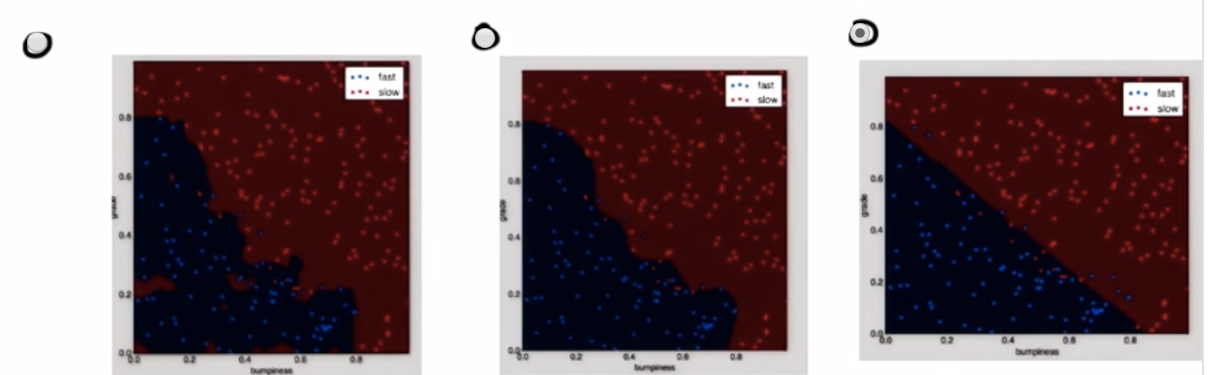
정답은 맨 오른쪽입니다. kernel 파라미터는 decision boundary의 모양을 선형으로 할지 다항식형으로 할지 등을 결정합니다. 사실 위 문제에서 gamma는 linear kernel에서 아무 영향이 없습니다. Reference4를 참고하시면 알 수 있습니다. linear식에는 Gamma(γ)가 없고, 나머지 poly, sigmoid, rbf에는 γ가 있습니다.
C
C : Controls tradeoff detween smooth decision boundary and classfying training points correctly
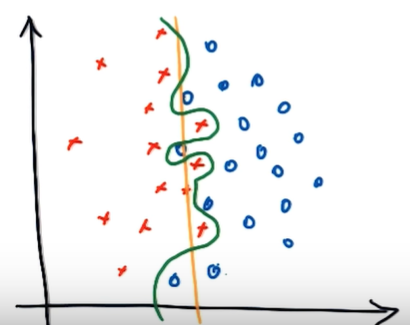
위 그래프에서 초록색 구분선은 C가 큰 decision boundary이고, 주황색 구분선은 C가 작은 decision boundary입니다. C가 크면 training 포인트를 정확히 구분해줍니다. 반면 C가 작으면 smooth한 decision boundary를 그려줍니다. 즉, C가 작으면 Margin이 커집니다. C는 training data를 정확히 구분할지 아니면 decision boundary를 일반화할지를 결정해줍니다. 결론적으로 C가 크면 decision boundary는 더 굴곡지고, C가 작으면 decision boundary는 직선에 가깝습니다.
Gamma(γ)
Gamma: Defines how far the influence of a single training point reaches
여기서 reach는 decision boudary의 굴곡에 영향을 주는 데이터의 범위이라고 보시면 됩니다. Gamma가 작다면 reach가 멀다는 뜻이고, Gamma가 크다면 reach가 좁다는 뜻입니다.
Gamma 값이 클 때
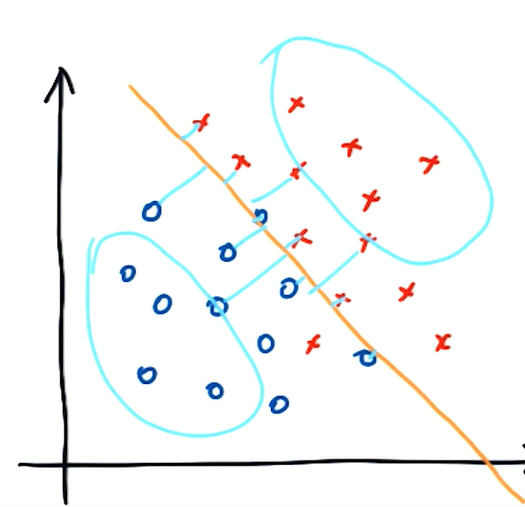
Gammar 값이 크다는 것은 위와 같이 reach가 좁다는 뜻입니다. reach가 좁기 때문에 원형 안에 있는 포인트는 decision boundary에 영향을 주지 않습니다. 따라서 decision boundary와 가까이 있는 포인트들만이 선의 굴곡에 영향을 줍니다. 그렇다면 decision boundary는 아래와 같이 굴곡지게 됩니다. 멀리 있는 포인트는 영향이 없으므로 선과 가까이 있는 포인트 하나하나의 영향이 상대적으로 크기 때문입니다.
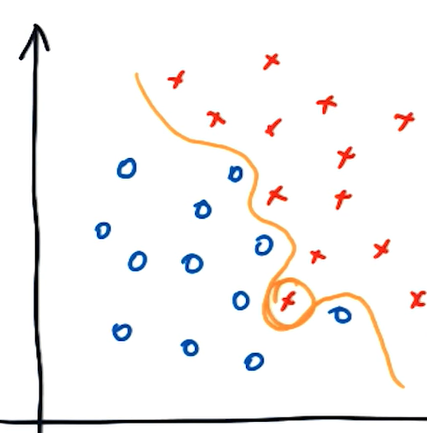
Gamma 값이 작을 때
Gamma 값이 작다면 reach가 멀기 때문에 대부분의 포인트가 decision boundary에 영향을 줍니다. 따라서 decision boundary와 가까이 있는 포인트 하나하나가 decision boundary에 주는 영향이 상대적으로 작습니다. 그래서 선이 포인트 하나 때문에 구부러지지 않습니다.
결론적으로 Gamma가 크면 decision boundary는 더 굴곡지고, Gamma가 작으면 decision boundary는 직선에 가깝습니다.
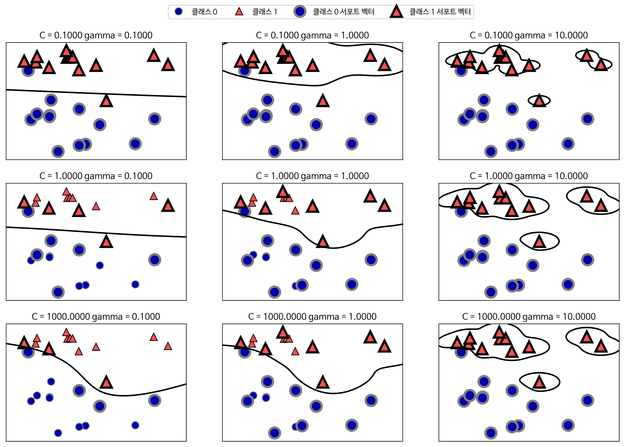
아래 그림을 통해 C와 Gamma에 따라 decision boundary가 어떻게 바뀌는지 참고하시기 바랍니다. 값이 커짐에 따라 C는 두 데이터를 정확히 구분하는 것에 초점이 두어져있고, Gamma는 개별 데이터마다 decision boundary를 만드는 것에 초점이 두어져 있습니다. 따라서 C는 아무리 커져도 decision boudnary는 하나입니다. (outlier가 없다면) 하지만 Gamma는 커짐에 따라 여러 decision boundary를 만듭니다.
오버피팅 (과적합, Overfitting)
오버피팅이란 훈련 데이터를 지나치게 학습하는 것을 뜻합니다. 오버피팅된 모델은 훈련 데이터에서는 100%에 가까운 성능을 내지만 테스트 데이터에서는 성능이 굉장히 떨어질 수 있습니다. 아래 그림을 보겠습니다.
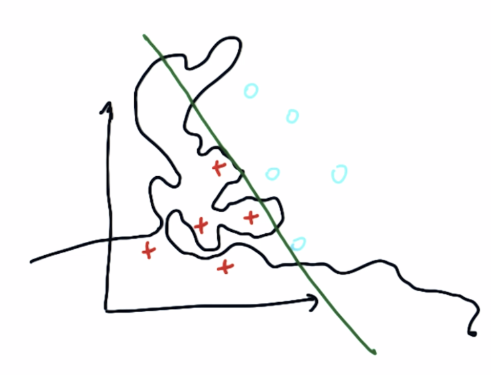
훈련 데이터를 과하게 학습하면 구불구불한 괴상한 decision boundary가 만들어집니다. 이는 올바른 decision boundary가 아닙니다. 직선으로 된 decision boundary가 더 적합하겠죠? Kerenl, C, Gamma 모두 오버피팅에 영향을 줄 수 있는 파라미터입니다. C와 Gamma를 지나치게 높게 잡는다면 오버피팅이 될 수 있습니다. 운동도 과하게 하면 오버트레이닝이 되어 근손실이 있을 수 있듯이, 머신러닝에서도 성능을 높히는 것과 오버피팅을 막는 것 사이의 균형을 잘 지켜야 합니다.
추가로, SVM은 training time이 길기 때문에 사이즈가 큰 데이터 셋에는 적합하지 않습니다. 또한 노이즈가 많은 데이터 셋에서는 오버피팅이 될 수 있어 적합하지 않습니다. 노이즈가 많을 경우에는 차라리 나이브 베이즈가 더 적합할 수 있습니다.
이상으로 서포트 벡터 머신(SVM)에 대해 알아봤습니다. 다음 포스트에서는 sklearn으로 실습을 해보겠습니다.
References
Reference2: SVM with polynomial kernel visualization
'머신러닝' 카테고리의 다른 글
| 머신러닝 - 5. 랜덤 포레스트(Random Forest) (6) | 2019.07.25 |
|---|---|
| 머신러닝 - 4. 결정 트리(Decision Tree) (31) | 2019.07.22 |
| 머신러닝 - 3. 서포트 벡터 머신 (SVM) 실습 (0) | 2019.07.18 |
| 머신러닝 - 1. 나이브 베이즈 분류 (Naive Bayes Classification) (20) | 2019.07.14 |
| Intro to Machine Learning (0) | 2019.07.13 |




