머신러닝 - 3. 서포트 벡터 머신 (SVM) 실습

sklearn을 활용하여 서포트 벡터 머신(SVM) 실습을 해보겠습니다. 코드 및 데이터는 제 깃헙에 모두 있습니다. 본 포스트의 내용은 OpenCV의 글을 정리한 것입니다. (Reference1)

Linearly Separable Data without Noise

먼저 가장 단순한 케이스를 봅시다. Noise가 전혀 없어 아주 깔끔하게 선형 구분이 가능한 데이터입니다.

Data without Noise

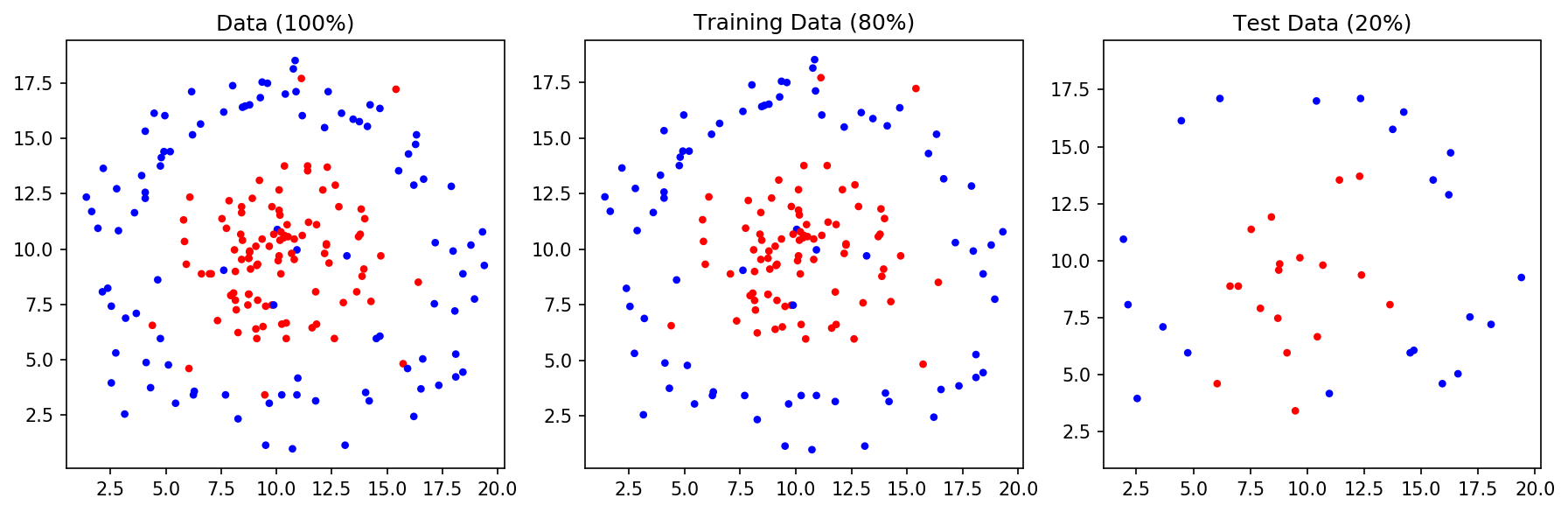
맨 왼쪽은 전체 데이터, 가운데는 Training Data, 오른쪽은 Test Data입니다. 전체 데이터를 80:20 비율로 Training Data, Test Data로 나눈 겁니다. Noise가 없고 딱 봐도 두 데이터를 선형(직선)으로 구분할 수 있습니다. SVM Classfier로 위 데이터를 구분하는 Decision Boundary를 그려보겠습니다. 나이브 베이즈와 마찬가지로 1. Classfier를 만들어주고, 2. 그 Classifier를 훈련시키고, 3. 마지막으로 테스트를 하면 됩니다. 아래 코드를 보면 나이브 베이즈와 거의 유사합니다. Classfier만 svm.SVC가 쓰였음을 알 수 있습니다.

# Read data
x, labels = read_data("points_class_0.txt", "points_class_1.txt")

# Split data to train and test on 80-20 ratio
X_train, X_test, y_train, y_test = train_test_split(x, labels, test_size = 0.2, random_state=0)

print("Displaying data. Close window to continue.")
# Plot data
plot_data(X_train, y_train, X_test, y_test)

# make a classifier and fit on training data
clf = svm.SVC(kernel='linear')

# Train classifier 
clf.fit(X_train, y_train)

print("Displaying decision function. Close window to continue.")  
# Plot decision function on training and test data
plot_decision_function(X_train, y_train, X_test, y_test, clf)

# Make predictions on unseen test data
clf_predictions = clf.predict(X_test)
print("Accuracy: {}%".format(clf.score(X_test, y_test) * 100 ))

kernel='linear'

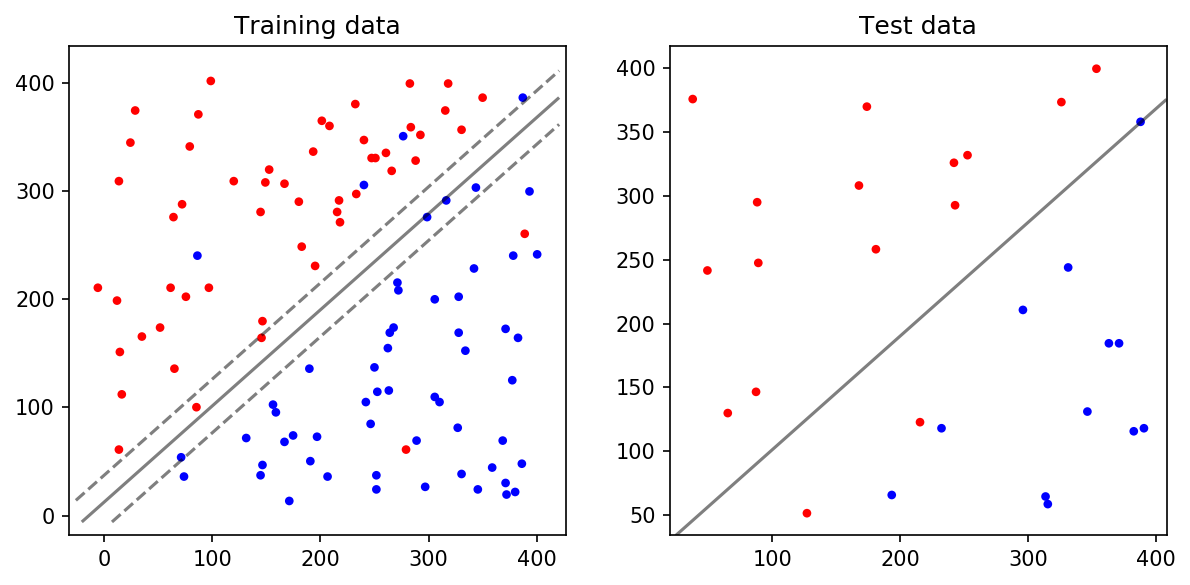
SVM을 활용하여 Decision Boundary를 구한 것입니다. 아주 단순하게 분류할 수 있기 때문에 kernel 파라미터를 'linear'로 했습니다. 

clf = svm.SVC(kernel='linear')

왼쪽의 Training Data에서 실선이 Decision Boundary이고, 점선이 Margin입니다. Training Data를 기반으로 만든 Decsion Bdoundary가 Test Data를 얼마나 잘 구분하는지를 봅시다. 오른쪽의 Test Data에서는 Decision Boundary가 100% 정확하게 빨간 점과 파란 점을 구분합니다. 따라서 Accuracy = 100.0%가 나옵니다.

Linearly Separable Data with Noise

이제는 조금 더 복잡한 데이터입니다. 빨간 점 사이에 파란 점이 조금씩 섞여 있습니다. 마찬가지로 파란 점 사이에 빨간 점이 섞여 있습니다. 이렇게 Noise가 조금씩 있으면 C 파라미터를 활용해서 Decision Boundary를 조절할 수 있습니다.

Data with Noise

# Read data
x, labels = read_data("points_class_0_noise.txt", "points_class_1_noise.txt")

# Split data to train and test on 80-20 ratio
X_train, X_test, y_train, y_test = train_test_split(x, labels, test_size = 0.2, random_state=0)

print("Displaying data. Close window to continue.")
# Plot data
plot_data(X_train, y_train, X_test, y_test)

# make a classifier and fit on training data
clf_1 = svm.SVC(kernel='linear', C=1)
clf_1.fit(X_train, y_train)

print("Display decision function (C=1) ...\nThe SVM classifier will choose a large margin decision boundary at the expense of larger number of misclassifications")
# Plot decision function on training and test data
plot_decision_function(X_train, y_train, X_test, y_test, clf_1)

# make a classifier and fit on training data
clf_100 = svm.SVC(kernel='linear', C=100)
clf_100.fit(X_train, y_train)

print("Accuracy(C=1): {}%".format(clf_1.score(X_test, y_test) * 100 ))
print("\n")
print("Display decision function (C=100) ...\nThe classifier will choose a low margin decision boundary and try to minimize the misclassifications")
# Plot decision function on training and test data
plot_decision_function(X_train, y_train, X_test, y_test, clf_100)

print("Accuracy(C=100): {}%".format(clf_100.score(X_test, y_test) * 100 ))

# Make predictions on unseen test data
clf_1_predictions = clf_1.predict(X_test)
clf_100_predictions = clf_100.predict(X_test)

kernel='linear', C = 1

kernel='linear', C = 100

위쪽은 C parameter를 1로 한 것이고, 아래는 100으로 한 것입니다. 앞선 포스트에서 설명했듯이 C를 작게 하면 훈련 데이터의 분류를 부정확하게 하는 대신 (= decision boundary를 곧게 그리는 대신) Margin을 크게 합니다. C를 크게 하면 Margin을 작게 하는 대신 훈련 데이터의 분류를 정확하게 (= decision boundray를 굴곡있게) 합니다.

If you set C to be a low value (say 1), the SVM classifier will choose a large margin decision boundary at the expense of larger number of misclassifications. When C is set to a high value (say 100), the classifier will choose a low margin decision boundary and try to minimize the misclassifications.

상황에 따라 C를 적절하게 선택해줘야 합니다. Noise가 많은 데이터라면 C를 작게 하는 것이 좋고, Noise가 별로 없는 데이터라면 C를 크게 하는 것이 좋습니다.

NonLinearly Separable Data with Noise

Non-linear Data with Noise

위 데이터는 Linear하게 분류할 수 없습니다. 따라서 앞선 포스트에서 설명한 것처럼 Kernel Trick을 활용해야 합니다. sklearn SVM에서는 Kernel Parameter를 통해 어떤 Kernel Trick을 활용할지 정할 수 있습니다. 또한 C와 gamma Parameter를 통해 decision boundary를 조절할 수 있습니다. 아래는 kernel='rbf', C=10, gamma=0.1인 예시입니다.

clf = svm.SVC(kernel='rbf', C = 10.0, gamma=0.1)

kernel='rbf', C=10, gamma=0.1

C와 gamma를 다양하게 조정해서 최적의 decision boundary를 찾는게 필요할 것입니다. Try & Error로 하나하나 직접 입력해주고 결과를 보고 하는 식으로 하면 시간도 많이 들고 번거롭겠죠. 하지만, 싸이킷런에서는 GridSearchCV라는 메서드가 이를 대신해줍니다. 최적의 파라미터를 찾아주는 놈입니다.

GridSearchCV는 3-fold cross-validation을 통해 파라미터의 성능을 평가합니다. 데이터를 세 파트로 나누어서 두 파트는 훈련 데이터로, 나머지 한 파트는 테스트 데이터로 활용합니다. 전체 데이터를 A, B, C 세 파트로 나누었다고 합시다. A, B는 훈련 데이터, C는 테스트 데이터로 해서 Accuracy를 평가합니다. 그 다음은 B, C를 훈련 데이터, A를 테스트 데이터로 합니다. 마지막으로 A, C를 훈련 데이터, B를 테스트 데이터로 합니다. 이렇게 세번의 Accuracy를 구해 평균을 취해줍니다. 하나의 파라미터에 대한 모델 성능(Accuracy)을 구할 때 매번 이렇게 해줍니다. 이것이 3-fold cross-validation입니다. 

# Read data
x, labels = read_data("points_class_0_nonLinear.txt", "points_class_1_nonLinear.txt")

# Split data to train and test on 80-20 ratio
X_train, X_test, y_train, y_test = train_test_split(x, labels, test_size = 0.2, random_state=0)

print("Displaying data.")
# Plot data 
plot_data(X_train, y_train, X_test, y_test)

print("Training SVM ...")
# make a classifier
clf = svm.SVC(C = 10.0, kernel='rbf', gamma=0.1)

# Train classifier
clf.fit(X_train, y_train)

# Make predictions on unseen test data
clf_predictions = clf.predict(X_test)

print("Displaying decision function.")
# Plot decision function on training and test data
plot_decision_function(X_train, y_train, X_test, y_test, clf)

# Grid Search
print("Performing grid search ... ")

# Parameter Grid
param_grid = {'C': [0.1, 1, 10, 100], 'gamma': [1, 0.1, 0.01, 0.001, 0.00001, 10]}

# Make grid search classifier
clf_grid = GridSearchCV(svm.SVC(), param_grid, verbose=1)

# Train the classifier
clf_grid.fit(X_train, y_train)

# clf = grid.best_estimator_()
print("Best Parameters:\n", clf_grid.best_params_)
print("Best Estimators:\n", clf_grid.best_estimator_)

print("Displaying decision function for best estimator.")
# Plot decision function on training and test data
plot_decision_function(X_train, y_train, X_test, y_test, clf_grid)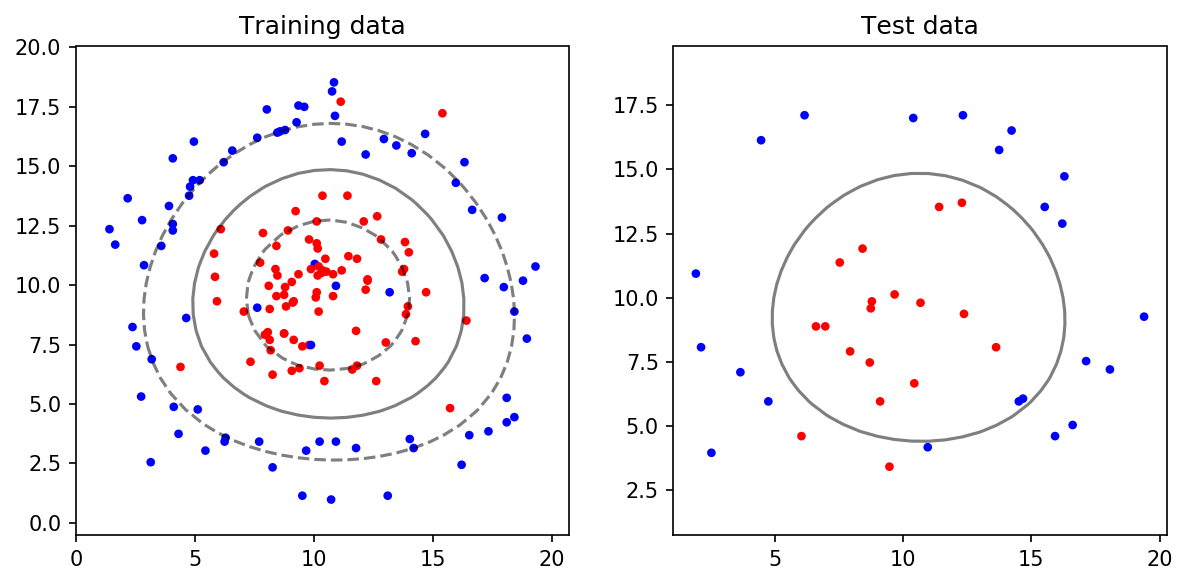

kernel='rbf', C=1, gamma=0.01

C=1, gamma=0.01일때 최적의 성능이 나왔습니다. 

Reference

Reference1: SVM using Scikit-Learn in Python

저작자표시비영리변경금지

• 카카오스토리
• 트위터
• 페이스북

'머신러닝' 카테고리의 다른 글

머신러닝 - 5. 랜덤 포레스트(Random Forest)  (6)	2019.07.25
머신러닝 - 4. 결정 트리(Decision Tree)  (27)	2019.07.22
머신러닝 - 3. 서포트 벡터 머신 (SVM) 실습  (0)	2019.07.18
머신러닝 - 2. 서포트 벡터 머신 (SVM) 개념  (10)	2019.07.15
머신러닝 - 1. 나이브 베이즈 분류 (Naive Bayes Classification)  (19)	2019.07.14
Intro to Machine Learning  (0)	2019.07.13