귀퉁이 서재
DATA - 11. 표본 분포, 대수의 법칙, 중심극한정리 본문

확률 변수, 확률 분포, 확률 표본, 표본 분포
우선, 용어에 대해서 확실하게 정리하고 넘어가겠습니다.
관심 대상인 모집단(Population)의 특성에 대해 알고자 할 때, 모집단 전체를 관찰할 수는 없습니다. 따라서 모집단으로부터 그 일부를 무작위로 뽑아 관측한 결과로부터 모집단 전체의 특성, 즉 모수(Parameter)를 추론하게 되는데, 이렇게 뽑은 모집단의 일부를 표본(Sample)이라고 합니다. 추론에는 통계량(Statistic)이라 불리는 표본의 함수가 사용되는데, 통계량의 분포, 즉 표본 분포를 알아야 합니다.
확률 변수(Random variable)란 무작위 실험을 했을 때, 특정 확률로 발생하는 각각의 결과를 수치 값으로 표현한 변수를 말합니다. (이름을 임의 변수라고 지었다면 직관적으로 이해하기 쉬웠을텐데...) 그리고 확률 분포(Probability distribution)란 확률 변수 X의 모든 값과 그에 대응하는 확률 값들의 분포를 말합니다. 확률 변수 X의 확률 분포 함수를 F라 하고, F 자체나 F의 모수를 모를 때, X의 관측값들을 통해 모수를 추론하게 됩니다. 만약 독립적으로 관측하여 얻는 n개의 값을 X1, X2,... ,Xn으로 나타낸다면, 이들은 서로 독립(independent)이고 X와 같은 분포 F를 따르게(identically distributed) 될 것입니다. (이를 동일 분포, 독립 분포라고 하며, 줄여서 iid(independent, identically distributed)라고 표기합니다.) 이 때 X1, X2, ... , Xn을 확률 변수 X에 대한 크기 n인 확률 표본(Random sample)이라고 합니다.
우리는 통계량을 이용하여 모수에 대한 통계적 추론을 하게 되는데, 이를 위해서는 통계량이 어떤 분포를 따르는지 알아야 합니다. 이때 통계량의 분포를 표본 분포(Sampling distribution)이라고 합니다. (Reference1: 통계학 이론과 응용, 배도선 저)
정규 분포를 따르는 모집단으로부터 크기 n인 표본을 추출하여 구한 표본 평균의 평균과 분산은 아래와 같습니다. (표본의 평균이 아닌 표본의 평균의 평균입니다.) (Reference2)

여기서, 모수와 통계량에 대한 notation은 아래와 같습니다. 모수 notation에 hat(^)을 다는 것도 통계량 notation입니다.

대수의 법칙 (Law of Large Numbers)
대수의 법칙(큰 수의 법칙, 라플라스의 정리라고도 함)이란 표본의 수가 많을수록(즉, n이 클수록) 표본평균이 모평균에 가까워진다는 이론입니다. 아래와 같이 numpy를 활용하여 확인해보겠습니다.
import numpy as np
np.random.seed(42)
# gamma분포로부터 무작위 표본 추출
pop_data = np.random.gamma(1,100,3000)
# 모평균
pop_data.mean()
>> 100.35978700795846
# 표본 갯수가 5, 20, 100, 10000일 때 표본 평균
np.random.choice(pop_data, 5).mean()
>> 27.685829640608965
np.random.choice(pop_data, 20).mean()
>> 163.3701520126447
np.random.choice(pop_data, 100).mean()
>> 119.55076984115861
np.random.choice(pop_data, 10000).mean()
>> 100.17760344212094모평균은 100.3598입니다. 표본의 개수가 작을수록 모평균과의 차이가 큽니다. 표본을 10,000개로 했더니 표본평균은 100.1776으로 모평균과 거의 일치했습니다.
중심극한정리 (Central Limit Theorem)
중심극한정리란 n이 클수록 확률 변수의 평균, proportion, 평균의 차이, proportion의 차이의 분포는 정규분포에 가까워진다는 이론입니다. 이는 분산과 correlation에는 적용이 안 됩니다. n이 클수록 확률 변수의 평균은 정규분포에 가까워진다는 것을 numpy를 통해 확인해보겠습니다.
n=3인 경우, n이 충분히 크지 않기 때문에 평균의 그래프 형태는 right-skewed입니다.
means_size_3 = []
for i in range(10000):
means_size_3.append(np.random.choice(pop_data, 3).mean())
plt.hist(means_size_3);
n=100인 경우에는 평균의 그래프 형태가 정규분포에 가깝습니다.
means_size_100 = []
for i in range(10000):
means_size_100.append(np.random.choice(pop_data, 100).mean())
plt.hist(means_size_100);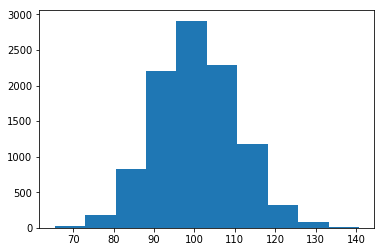
# 모평균
pop_data.mean()
>> 100.35978700795846
# 표본평균
np.mean(means_size_100)
>> 100.42914539368782
# 모분산
pop_data.var()
>> 9955.7693930654896
# 표본분산
np.var(means_size_100)
>> 99.459805370845459n=100인 경우에 모평균과 표본평균은 거의 일치하고, 표본분산은 모분산의 1/100입니다. n=100이기 때문에, 위 공식에 의해 분산 값이 작아졌습니다.
References
Reference1 : 통계학 이론과 응용, 배도선 저
'데이터 분석' 카테고리의 다른 글
| DATA - 13. 가설검정과 p-value, 본페로니 교정 (6) | 2019.04.19 |
|---|---|
| DATA - 12. 부트스트랩(Bootstrap) (10) | 2019.04.16 |
| DATA - 10. 베이즈 추정(Bayesian Estimation) (8) | 2019.04.13 |
| DATA - 9. 베르누이 시행과 이항 분포 (0) | 2019.04.12 |
| DATA - 8. 심슨의 역설 (0) | 2019.04.11 |




