귀퉁이 서재
DATA - 10. 베이즈 추정(Bayesian Estimation) 본문

기하학에 피타고라스 정리가 있다면 확률론에는 베이즈 정리가 있다.
- 해럴드 제프리스 경
해럴드 제프리스 경이 말한 것처럼 베이즈 정리는 인공지능과 통계학에 지대한 영향을 끼친 중요한 통계학 이론입니다.
베이즈 추정이란?
협력업체로부터 납품받은 기계의 성능을 평가한다고 해봅시다. 그러기 위해서는 납품받은 몇 개의 부품을 무작위로 뽑아 이 표본에서 얻어진 정보만으로 모수(협력업체로부터 납품받은 기계 전체)의 성능을 평가해야 합니다. 하지만 과거 납품 시 성능검사기록이나 비슷한 부품의 성능 자료, 이 부품의 물리적 특성에 관한 지식 등을 통해 이 부품의 사전 정보를 얻을 수도 있습니다. 이런 경우 단순히 표본을 통해 모수를 추정하기보다는 표본 정보와 사전 정보를 함께 사용하여 모수를 추정하는 것이 보다 바람직할 것입니다. (Reference1: 통계학 이론과 응용, 배도선 저)
이와 같이 추론 대상의 사전 확률과 추가적인 정보를 기반으로 해당 대상의 사후 확률을 추론하는 통계적 방법을 베이즈 추정(Bayesian Estimation)이라고 합니다. (Reference2)
베이즈 추정은 아래와 같이 계산할 수 있습니다.
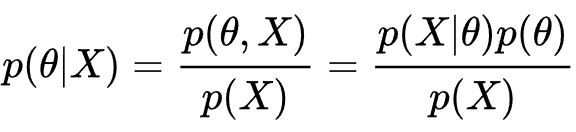
사례를 들어보겠습니다. 어떤 마을 전체 사람들의 10.5%가 암 환자이고, 89.5%가 암 환자가 아닙니다. 이 마을의 모든 사람에 대해 암 검진을 실시했다고 합시다. 암 검진시 양성 판정, 음성 판정 결과가 나올 수 있습니다. 하지만 검진이 100% 정확하지는 않고 약간의 오차가 있습니다. 암 환자 중 양성 판정을 받은 비율은 90.5%, 암 환자 중 음성 판정을 받은 비율은 9.5%, 암 환자가 아닌 사람 중 양성 판정을 받은 비율은 20.4%, 암 환자가 아닌 사람 중 음성 판정을 받은 비율은 79.6%입니다. 어떤 사람이 양성 판정을 받았을 때 이 사람이 암 환자일 확률은 얼마일까요?
우선 이를 수식으로 표현해보겠습니다.
약자 - C: Cancer(암 환자), P: Positive(양성), N: Negative(음성)
P(C): 암 환자일 확률 = 0.105
P(~C): 암 환자가 아닐 확률 = 0.895
P(P|C): 암 환자일 때 양성 판정을 받을 확률 = 0.905 (이를 민감도라고 합니다. sensitivity)
P(N|C): 암 환자일 때 음성 판정을 받을 확률 = 0.095
P(P|~C): 암 환자가 아닐 때 양성 판정을 받을 확률 = 0.204
P(N|~C): 암 환자가 아닐 때 음성 판정을 받을 확률 = 0.796 (이를 특이도라고 합니다. specificity)
이때 P(C|P): 어떤 사람이 양성 판정을 받았을 때 이 사람이 암 환자일 확률은?
베이즈의 추정에 의해
P(C|P) = P(P|C)*P(C) / P(P)
여기서, P(P) = P(P, C) + P(P, ~C) = P(P|C)*P(C) + P(P|~C)*P(~C)입니다.
P(P), 즉 양성 판정을 받을 확률은 암 환자이자 양성 판정을 받을 확률(P(P, C))과 암 환자가 아닌데 양성 판정을 받을 확률(P(P, ~C))의 합과 같습니다.
조건부 확률에 의해 P(P, C) = P(P|C)*P(C)이고, P(P, ~C) = P(P|~C)*P(~C)입니다.
따라서, P(C|P) = P(P|C)*P(C) / P(P) = 0.905*0.105 / (0.905*0.105 + 0.204*0.895) = 0.342입니다.
P(C|P), P(C|N), P(C|N)도 마찬가지로 계산하면 각각 0.65797, 0.013808, 0.986192가 나옵니다. 이제, python pandas를 활용하여 직접 계산해보겠습니다.
# load dataset
import pandas as pd
df = pd.read_csv('cancer_test_data.csv')
df.head()| patient_id | test_result | has_cancer | |
|---|---|---|---|
| 0 | 79452 | Negative | False |
| 1 | 81667 | Positive | True |
| 2 | 76297 | Negative | False |
| 3 | 36593 | Negative | False |
| 4 | 53717 | Negative | False |
# 양성 판정 받은 사람 중 암 환자일 확률: P(C|P)
df.query('test_result == "Positive"').has_cancer.mean()0.34282178217821785# 양성 판정 받은 사람 중 암 환자가 아닐 확률: P(~C|P)
(df.query('test_result == "Positive"')['has_cancer'] == False).mean()0.65717821782178221# 음성 판정 받은 사람 중 암 환자일 확률: P(C|N)
df.query('test_result == "Negative"').has_cancer.mean()0.013770180436847104# 음성 판정 받은 사람 중 암 환자가 아닐 확률: P(~C|N)
(df.query('test_result == "Negative"')['has_cancer'] == False).mean()0.98622981956315292실제 데이터를 pandas로 계산한 결과와 베이즈 추정으로 계산한 결과가 같은 것을 볼 수 있습니다. 암 환자는 양성 판정을 받을 확률이 높습니다. 하지만 양성 판정을 받았어도 암이 아닐 확률이 더 높다는 걸 알 수 있습니다.
References
Reference1: 통계학 이론과 응용, 배도선 저
'데이터 분석' 카테고리의 다른 글
| DATA - 12. 부트스트랩(Bootstrap) (10) | 2019.04.16 |
|---|---|
| DATA - 11. 표본 분포, 대수의 법칙, 중심극한정리 (0) | 2019.04.14 |
| DATA - 9. 베르누이 시행과 이항 분포 (0) | 2019.04.12 |
| DATA - 8. 심슨의 역설 (0) | 2019.04.11 |
| DATA - 7. 분산과 표준편차에서 n이 아니라 n-1로 나누는 이유 (자유도) (8) | 2019.04.10 |




