귀퉁이 서재
DATA - 9. 베르누이 시행과 이항 분포 본문

우선 이항 분포를 위키피디아에서 검색해보겠습니다.
이항 분포는 연속된 n번의 독립적 시행에서 각 시행이 확률 p를 가질 때의 이산 확률 분포이다. 이러한 시행은 베르누이 시행이라고 불리기도 하며, n=1일 때 이항 분포를 베르누이 분포라고도 한다.
동전을 던지거나 시험을 보는 경우 나타날 수 있는 결과의 집합은 {앞면, 뒷면}, {합격, 불합격}으로 둘밖에 없습니다. 이와 같이 나올 수 있는 결과가 둘 뿐인 확률 실험을 베르누이 실험(Bernoulli experiment)이라고 하고, 동일한 베르누이 실험을 반복할 때 각각의 실험을 베르누이 시행(Bernoulli trial)이라고 합니다. 베르누이 분포는 매우 단순하기 때문에 그 자체보다는, 베르누이 시행을 독립적으로 반복하여 나타나는 여러 분포들을 유추하는데 중요한 의미가 있습니다. 성공 확률은 p, 실패 확률은 1-p인 베르누이 시행을 독립적으로 n번 반복할 때 성공이 k번, 실패가 (n-k)번 나올 확률을 구하면 아래와 같습니다. (Reference: 통계학 이론과 응용, 배도선 저)
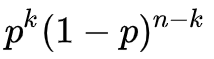
또한, 성공이 k번, 실패가 (n-k)번 나오는 모든 배열의 수는

입니다.
이때 확률변수 K의 확률 함수는

입니다. 이때 K는 모수가 n과 p인 이항 분포(binomial distribution)를 따른다고 하고, K ~ B(n, p)라고 표기합니다. 만약 X ~ B(n, p)라면, X의 평균 E(X) = np, 그리고 X의 분산 Var(X) = np(1-p)입니다.
이항 분포는 numpy를 활용해 쉽게 구현할 수 있습니다.
import numpy as np
tests = np.random.binomial(1, 0.5, 100000)
(tests == 1).mean()0.49987700000000002np.random.binomial(1, 0.5, 1000000)에서 1은 반복 횟수 n, 0.5는 성공 확률 p, 1000000은 반복 횟수가 n이고, 성공 확률이 p인 시행 자체를 1000000번 거듭한다는 뜻입니다. 동전은 한번 던지면 뒷면(0) 또는 앞면(1)이 나옵니다. 한번 던져서 0이 나오면 0을 기록하고 1이 나오면 1을 기록하며 1000000번을 반복하는 겁니다. tests는 array(\[0, 1, 0,..., 1, 0, 0\])가 될 것이며, 이 array의 평균을 구하면 이항 분포의 기댓값(평균)이 됩니다. 예상한 대로 n=1, p=0.5이므로 평균은 np = 1*0.5 = 0.5 (코드 결과에서는 0.49987700000000002)입니다.
# n=10, p=0.15 / 1000000번 반복 시행
tests = np.random.binomial(10, 0.15, 1000000)
# 앞면이 3번 이상 나올 확률
(tests >= 3).mean()0.17944199999999999앞면이 3번 이상 나올 확률은 전체 확률에서 앞면이 2번 이하 나올 확률을 빼면 됩니다.
1-P(X<=2) = 1- {P(X=0)+P(X=1)+P(X=2)}
P(X=0), P(X=1), P(X=2)는 확률 함수에 대입해 구할 수 있으며, np.random.binomial은 이를 간단히 계산해줍니다.
References
Reference2 : 통계학 이론과 응용, 배도선 저
'데이터 분석' 카테고리의 다른 글
| DATA - 11. 표본 분포, 대수의 법칙, 중심극한정리 (0) | 2019.04.14 |
|---|---|
| DATA - 10. 베이즈 추정(Bayesian Estimation) (8) | 2019.04.13 |
| DATA - 8. 심슨의 역설 (0) | 2019.04.11 |
| DATA - 7. 분산과 표준편차에서 n이 아니라 n-1로 나누는 이유 (자유도) (8) | 2019.04.10 |
| DATA - 6. 기술 통계학과 추측 통계학 (0) | 2019.04.08 |



