귀퉁이 서재
DATA - 15. p-value의 함정 본문

p-value에 대해서는 앞선 챕터에서 간단히 알아봤습니다. 본 챕터에서는 p-value가 가지고 있는 함정에 대해 알아볼 것입니다. 바로 이전 챕터에서 설명한 것처럼, 통계적 유의성이 항상 실질적 유의성으로 귀결되는 것은 아닙니다. 또한, p-value를 통계적 유의성을 판단할 수 있는 중요한 지표 중 하나로 생각해야지, p-value 자체를 연구의 목적으로 생각해서는 안됩니다. 하지만, 유의미한 p-value를 도출하기 위해 가설검정 자체를 조작하는 연구자들도 간혹 있다고 합니다. p-value는 통계적 유의성의 척도(measure)이지, p-value 자체가 목적(target)은 아닙니다.
"When a measure become a target, it is no longer a measure“.
일반적으로 p-value를 구해 통계적 유의성을 검증하고 이를 기반으로 실질적 유의성을 따집니다. 통계적 유의성 자체도 함정이 있지만 p-value도 함정이 있다는 점을 알아야 합니다. 단지 통계적으로 유의한 결과를 도출하기 위해 혹은 유의미한 p-value를 도출하기 위해 상황에 맞지 않는 테스트를 하는 것은 결국엔 해가 될 것입니다.
동일한 문제라도 귀무가설과 대립가설을 어떻게 설정하는가에 따라 p-value가 달라질 수 있습니다. 아래 예제를 통해 가설에 따라 p-value가 어떻게 달라지는지 알아보겠습니다. 본 예제는 (Reference2)에서 가져왔습니다.
장남 혹은 장녀(이하 '맏'이라 표현)이 동생들보다 IQ가 높은지 검증을 해보는 예제입니다. 일반적으로 '차이가 없다'가 귀무가설로 많이 쓰입니다. 즉, '맏과 동생들의 IQ차이가 0이다'입니다. 계산할 통계량이 맏의 평균 IQ와 동생들의 평균 IQ 차이입니다. 귀무가설이 '차이는 0이다'이므로, 평균이 0이고, 표준편차는 0.75인 분포를 그려보겠습니다. (0.75는 모표준편차입니다. 모표준편차대신 부트스트랩을 활용한 표본 표준편차를 사용할 수도 있습니다.)
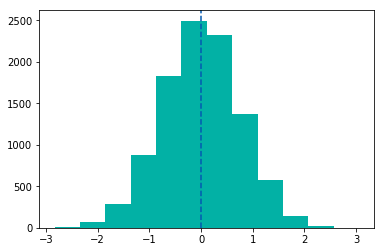
가설1: 맏이 동생들보다 IQ가 높다. (Eldest Children have Higher IQs)
H0:μ_eldest- μ_non-eldest≤ 0
H1:μ_eldest- μ_non-eldest> 0
즉,
귀무가설: 맏의 평균 IQ와 동생의 평균 IQ의 차이는 0보다 작거나 같다.
대립가설: 맏의 평균 IQ와 동생의 평균 IQ의 차이는 0보다 크다.
일반적으로 귀무가설에는 등호(=)가 포함되어 있습니다.
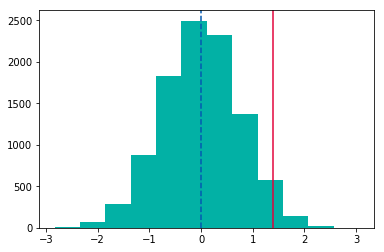
표본을 추출해 맏의 평균 IQ와 동생의 평균 IQ 차를 구하니 1.4가 나왔다고 합시다. 빨간 선은 평균 IQ 차이에 대한 관측 값입니다. p-value는 빨간 선 오른쪽 영역의 넓이와 같습니다. 오른쪽 영역인지 왼쪽 영역인지는 대립가설의 부등호 방향에 따라 결정됩니다. (이전 챕터의 p-value를 참고하시기 바랍니다.)
p_value = (dist > 1.4).mean()dist > 1.4 는 boolean 값으로 True 혹은 False가 나올 것이고, True면 1, False면 0으로 계산이 됩니다. 이것의 mean()을 구하면 1.4보다 큰 dist의 비율이 구해집니다. p-value는 귀무가설이 참이라고 가정했을 때, 관측값과 같거나 더 극단적인 값이 나올 확률 입니다. 따라서 (dist > 1.4).mean()은 p-value가 됩니다. 계산해보니 p-value가 0.0294가 나옵니다. 유의수준 0.05 하에서 귀무가설을 기각해야 합니다. 따라서 맏이 동생들보다 IQ가 높다고 할 수 있습니다.
가설2: 맏이 동생들보다 IQ가 낮다. (Eldest Children have Lower IQs)
H0:μ_eldest- μ_non-eldest ≥ 0
H1:μ_eldest- μ_non-eldest < 0
즉,
귀무가설: 맏의 평균 IQ와 동생의 평균 IQ의 차이는 0보다 크거나 같다.
대립가설: 맏의 평균 IQ와 동생의 평균 IQ의 차이는 0보다 작다.
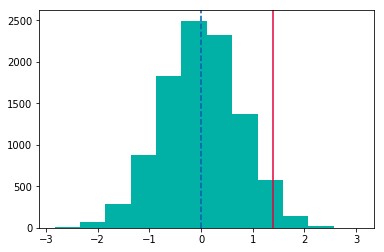
가설1과 마찬가지로 맏의 평균 IQ와 동생의 평균 IQ 차는 1.4입니다. 이 때, p-value는 빨간 선 왼쪽 영역의 넓이와 같습니다.
p_value = (dist < 1.4).mean()p-value는 0.9706입니다. 귀무가설을 기각하지 못합니다. 즉, 맏이 동생들보다 IQ가 같거나 높다고 할 수 있습니다.
가설3: 맏과 동생들의 IQ 차이가 있다. There is a difference in the IQs of eldest children and their younger siblings)
H0:μ_eldest- μ_non-eldest = 0
H1:μ_eldest- μ_non-eldest ≠ 0
즉,
귀무가설: 맏의 평균 IQ와 동생의 평균 IQ간 차이가 없다.
대립가설: 맏의 평균 IQ와 동생의 평균 IQ간 차이가 있다.

맏의 평균 IQ와 동생의 평균 IQ 차는 위 두 가설과 동일하게 1.4입니다. 이 때, p-value는 오른쪽 빨간 선의 오른쪽 영역 넓이와 왼쪽 빨간 선의 왼쪽 영역 넓이와 합과 같습니다.
p_upper = (dist > 1.4).mean()
diff_means = 0 - 1.4
lower_compare = 0 + diff_means
p_lower = (dist < lower_compare).mean()
p_val = p_upper + p_lowerp_upper = 0.0294, p_lower = 0.0321입니다. 따라서, p_val = 0.0615입니다. p-value가 0.0615이므로 유의수준 0.05하에서 귀무가설을 기각하지 못합니다. 따라서 맏의 평균 IQ와 동생의 평균 IQ간 차이가 없다고 할 수 있습니다.
이상하네요? 가설1에서는 맏의 평균 IQ가 동생들의 평균IQ보다 높다는 결론이 나왔는데, 가설3에서는 두 IQ에 차이가 없다는 결론이 나왔습니다. 가설을 어떻게 설정하느냐에 따라 p-value가 달라져 통계적 유의성에도 영향을 줄 수 있습니다. 이에 대해서 reference의 글귀를 그대로 가져왔으니 참고하시기 바랍니다. 여기서 direction은 부등호를 가진 가설을 의미합니다.
One of the interesting things here is the impact of not selecting a direction in our hypothesis. If we select a direction, we have more 'space' within which to find a p-value that is lower than our α level when compared to when we are just looking for a difference. (This is why when I did my stats education they strongly suggested that we used hypotheses that looked for a difference rather than a direction. You had to be VERY sure that you expected a certain direction if you wanted to pick that to prevent a greater chance of Type I errors.)
어떤 가설을 설정하는가, 표본의 크기를 얼마나 크게하는가에 따라 p-value가 달라지고 그에 따라 통계적 유의성이 달라질 수 있음을 알았습니다.
References
'데이터 분석' 카테고리의 다른 글
| DATA - 17. 최소자승법(OLS)을 활용한 단순 선형 회귀 (Simple Linear Regression) (8) | 2019.04.28 |
|---|---|
| DATA - 16. A/B Test (4) | 2019.04.25 |
| DATA - 14. 통계적 유의성의 함정 (0) | 2019.04.23 |
| DATA - 13. 가설검정과 p-value, 본페로니 교정 (6) | 2019.04.19 |
| DATA - 12. 부트스트랩(Bootstrap) (10) | 2019.04.16 |




