귀퉁이 서재
DATA - 16. A/B Test 본문

A/B Test
A/B Test는 마케팅이나 웹 페이지 개선에 많이 쓰이는 테스트 기법입니다. 기존의 웹페이지를 새로운 디자인으로 바꾸기 전에 이 디자인이 정말 고객에게 효과가 있는지를 먼저 판단해야 할 것입니다.기존의 웹페이지(A)와 새로 디자인된 웹페이지(B)가 있을 때, 새로 디자인된 웹페이지가 더 효과가 있는지(고객을 더 많이 유입하는지, 고객의 클릭률을 더 많이 유도하는지, 구매율을 높이는지, 고객 만족도를 높이는지 등)를 테스트하는 것이 A/B test입니다. 특정 그룹에는 기존 웹페이지만 보여주고, 또 다른 특정 그룹에는 새로 디자인된 웹페이지를 보여줍니다. 여기서 기존 웹페이지를 보는 그룹을 대조군, 새로운 웹페이지를 보는 그룹을 실험군이라고 합니다. 귀무가설과 대립가설은 아래와 같습니다.
귀무가설: 새로운 웹페이지가 기존 웹페이지보다 효과가 덜 하거나 차이가 없다.
대립가설: 새로운 웹페이지가 더 효과적이다.
가설검정을 통해 귀무가설을 기각하면 새로운 웹페이지가 더 효과적이라고 판단하여 디자인을 교체할 수 있습니다.
A/B tset를 왜 이런 식으로 할까요?
다른 방식의 예를 들어보겠습니다. 1월부터 5월까지는 모든 고객에게 기존 웹페이지를 노출합니다. 새로운 웹페이지를 테스트하기 위해 6월부터 10월까지는 모든 고객에게 새로운 웹페이지를 노출합니다. 이때 새로운 웹페이지의 유입률, 클릭률, 구매율, 만족도 등이 높다고 해서 '새로운 웹페이지가 더 효과적이다'라고 말할 수 있을까요? 아닙니다. 1~5월과 6~10월이라는 계절별, 월별 차이가 있을 수 있고, 시간이 지남에 따라 사회 경제적 차이가 있을 수 있습니다. 웹페이지 디자인 이외에도 변동되는 요소들이 많기 때문에 순수하게 웹페이지 디자인의 영향인지 알 수가 없습니다. 따라서 나머지 조건은 모두 동일하게 고정하고 디자인의 차이만을 분석하기 위해 동일한 기간에 대조군과 실험군을 나누어 웹페이지를 노출하는 것입니다.
Change Aversion vs Novelty Effect
하지만, A/B 테스트에도 Change Aversion, Novelty Effect라는 문제가 있을 수 있습니다. 어떤 변화가 있을 때, 그 변화의 효과와는 무관하게 거부감이 들고, 반감을 표하는 사람들도 있습니다. 단지 변화를 싫어하는 것입니다. 이를 Change Aversion이라고 합니다. 반대로, 변화를 무작정 반기는 사람들도 있습니다. 정말 효과적인지를 떠나 새로운 것이라면 좋아하는 것입니다. 이를 Novelty Effect라고 합니다.
A/B Test 실습
실제 데이터를 활용하여 A/B test 실습을 해보겠습니다. 실습에 앞서 CTR이라는 용어를 먼저 정의하고 가겠습니다. CTR(Click through rate)이란 노출 대비 클릭률을 의미합니다.
CTR = number of clicks by unique users / number of views by unique users
본 실습에서는 새로운 웹 페이지의 CTR이 기존 웹 페이지의 CTR보다 더 높은지 검정해보겠습니다. A/B Test 가설검정의 프로세스는 앞선 챕터에서 했던 것과 동일한 방식이며, 아래와 같습니다.
1. 대조군과 실험군 CTR의평균 차이를 구합니다. (관측값, observed value)
2. 부트스트랩을 활용하여 대조군과 실험군의 표본 CTR 평균의 차이를 구합니다. (부트스트랩 반복 횟수만큼 list에 저장)
3. 귀무가설이 참이라 가정하고, 중심은 귀무가설에서 가정한 평균(여기서는 0), 표준편차는 모표준편차 혹은 부트스트랩을 활용하여 구한 표본표준편차를 가지는 정규분포를 그립니다.
4. 정규분포와 관측값을 통해 p-value를 구합니다.
5. 구한 p-value를 통해 통계적 유의성을 검증합니다.
본 실습의 가설은 CTR과 관련 있으므로 다음과 같습니다.
귀무가설: 새로운 웹페이지의 평균 CTR이 기존 웹페이지의 평균 CTR보다 낮거나 차이가 없다.
대립가설: 새로운 웹페이지의 평균 CTR이 더 높다.
데이터 셋은 제 깃헙에 있습니다. (Data set)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
% matplotlib inline
np.random.seed(42)
df = pd.read_csv('course_page_actions.csv')
df.head()| timestamp | id | group | action | duration |
| 2016-09-24 17:14:52.012145 | 261869 | experiment | view | 130.545004 |
| 2016-09-24 18:45:09.645857 | 226546 | experiment | view | 159.862440 |
| 2016-09-24 19:16:21.002533 | 286353 | experiment | view | 79.349315 |
| 2016-09-24 19:43:06.927785 | 842279 | experiment | view | 55.536126 |
| 2016-09-24 21:08:22.790333 | 781883 | experiment | view | 204.322437 |
action column에는 'view'와 'enroll' 값이 있습니다. view는 웹페이지를 단지 본 것이고, enroll은 등록버튼을 클릭한 것입니다. 즉, enroll 개수 대비 view 개수가 CTR이 되는 것입니다. 대조군(control group)과 실험군(experiment group)의 평균 CTR 차이를 구해보겠습니다. 그다음, 부트스트랩을 통해 얻어진 CTR 차이 분포를 그래프로 그려보겠습니다.
# Get dataframe with all records from control group
control_df = df.query('group == "control"')
# Compute click through rate for control group
control_ctr = control_df.query('action == "enroll"').id.nunique() / control_df.query('action == "view"').id.nunique()
# Display click through rate
control_ctr
>> 0.2364438839848676
# Get dataframe with all records from control group
experiment_df = df.query('group == "experiment"')
# Compute click through rate for experiment group
experiment_ctr = experiment_df.query('action == "enroll"').id.nunique() / experiment_df.query('action == "view"').id.nunique()
# Display click through rate
experiment_ctr
>> 0.2668693009118541
# Compute the observed difference in click through rates
obs_diff = experiment_ctr - control_ctr
# Display observed difference
obs_diff
>> 0.030425416926986526
# Create a sampling distribution of the difference in proportions
# with bootstrapping
diffs = []
size = df.shape[0]
for _ in range(10000):
b_samp = df.sample(size, replace=True)
control_df = b_samp.query('group == "control"')
experiment_df = b_samp.query('group == "experiment"')
control_ctr = control_df.query('action == "enroll"').id.nunique() / control_df.query('action == "view"').id.nunique()
experiment_ctr = experiment_df.query('action == "enroll"').id.nunique() / experiment_df.query('action == "view"').id.nunique()
diffs.append(experiment_ctr - control_ctr)
# Convert to numpy array
diffs = np.array(diffs)
# Plot sampling distribution
plt.hist(diffs);
그 다음은, 귀무가설을 기반으로 하는 정규분포를 그립니다. (평균은 0 (차이가 없다), 표준편차는 부트스트랩 표본의 표준편차)
# Simulate distribution under the null hypothesis
null_vals = np.random.normal(0, diffs.std(), diffs.size)
# Plot the null distribution
plt.hist(null_vals);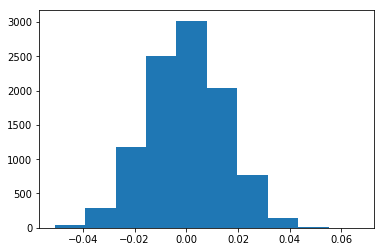
# Plot observed statistic with the null distibution
plt.hist(null_vals);
plt.axvline(obs_diff, c='red')
맨 처음 구했던 실험군과 대조군의 평균 CTR 차이에 해당하는 값을 빨간 선으로 표시했습니다.
# Compute p-value
(null_vals > obs_diff).mean()
>> 0.018800000000000001유의수준(α)이 0.05일 때, 귀무가설을 기각합니다. 따라서, 새로운 웹페이지의 평균 CTR이 더 높다고 판정 내릴 수 있습니다.
'데이터 분석' 카테고리의 다른 글
| DATA - 18. 다중 선형 회귀 (Multiple linear regression) (4) | 2019.04.30 |
|---|---|
| DATA - 17. 최소자승법(OLS)을 활용한 단순 선형 회귀 (Simple Linear Regression) (8) | 2019.04.28 |
| DATA - 15. p-value의 함정 (2) | 2019.04.24 |
| DATA - 14. 통계적 유의성의 함정 (0) | 2019.04.23 |
| DATA - 13. 가설검정과 p-value, 본페로니 교정 (6) | 2019.04.19 |




