귀퉁이 서재
DATA - 20. 다중공선성(Multicollinearity)과 VIF(Variance Inflation Factors) 본문
DATA - 20. 다중공선성(Multicollinearity)과 VIF(Variance Inflation Factors)
Baek Kyun Shin 2019. 5. 1. 13:03
이번 시간에는 다중공선성과 VIF에 대해 알아보겠습니다.
독립 변수 X는 종속 변수 Y 하고만 상관 관계가 있어야 하며, 독립 변수끼리 상관 관계가 있어서는 안 됩니다. 독립 변수간 상관 관계를 보이는 것을 다중공선성(Multicollinearity)이라고 합니다. 다중공선성이 있으면 부정확한 회귀 결과가 도출됩니다. (X와 Y의 상관 관계가 반대로 나온다던가 검정 결과가 다르게 나온다던가 말이죠.)
회귀 모델에 다중공선성이 있는지 파악하는 방법은 두 가지가 있습니다.
1. 산점도 그래프 (Scatter plot Matrix)
2. VIF (Variance Inflation Factors, 분산팽창요인)
산점도 그래프를 통해 독립 변수끼리 상관 관계가 있는지 파악하는 방법에 대해서는 아래 Python 코드 실습에서 살펴보겠습니다.
VIF는 다중 회귀 모델에서 독립 변수간 상관 관계가 있는지 측정하는 척도입니다. (Reference1) 수식은 아래와 같습니다.

위 식에서 R² (결정계수)에 대해 궁금하신 분들은 이전 챕터 (DATA - 17. 최소자승법(OLS)을 활용한 단순 선형 회귀(Simple Linear Regression))(Simple Linear Regression)) 아래 쪽을 참고해주시기 바랍니다.
VIF가 10이 넘으면 다중공선성 있다고 판단하며 5가 넘으면 주의할 필요가 있는 것으로 봅니다. 독립 변수 a와 b가 서로 상관 관계가 있다고 했을 때 두 변수 모두 VIF가 높습니다. 어느 하나만 VIF가 높은 경우는 없습니다. 박수도 오른손과 왼손이 있어야 칠 수 있듯이 서로 연관 있는 변수끼리 VIF가 높습니다. 아래 예제를 통해 자세히 알아보겠습니다.
다중공선성과 VIF 실습
파이썬을 활용하여 다중공선성과 VIF에 대해 실습해보겠습니다. seaborn, dmatirces, variance_inflation_factor 라이브러리가 추가되었습니다.
import pandas as pd
import numpy as np
import seaborn as sns
from patsy import dmatrices
import statsmodels.api as sm;
from statsmodels.stats.outliers_influence import variance_inflation_factor
%matplotlib inline
df = pd.read_csv('house_prices.csv')
df.head()
데이터는 이전 챕터에서 실습했던 것과 동일합니다. 지역(neighborhood), 집 크기(area), 침실 개수(bedrooms), 화장실 개수(bathrooms), 집 스타일(style)에 따라 집 값(price)가 어떻게 변하는지 나타내는 데이터입니다. 역시 제 깃헙에서 받아가실 수 있습니다.
다중공선성을 파악할 수 있는 방법 중 하나는 산점도(Scatter plot)를 그리는 것입니다. 침실 개수(bedrooms), 화장실 개수(bathrooms), 집 크기(area) 간 상관 관계가 있는지 Scatter plot으로 알아보겠습니다. sns.pairplot을 통해 독립 변수간 1대 1 상관 관계를 눈으로 파악할 수 있습니다. (Reference2)
sns.pairplot(df[['bedrooms', 'bathrooms', 'area']]);
bathrooms, bedrooms, area간 1대 1 상관 관계입니다. 2행 1열은 bathrooms와 bedrooms간의 그래프입니다. 강한 양의 상관 관계가 있는 것을 볼 수 있습니다. bathrooms가 많으면 bedrooms도 많다는 뜻입니다. 1행 2열은 2행 1열 그래프에서 x와 y의 축만 바꾼 것입니다. 3행 1열에서도 bedrooms와 area가 양의 상관 관계가 있는 것을 볼 수 있습니다. bathrooms와 area도 마찬가지도 양의 상관 관계입니다. 가장 강한 상관 관계를 보이는 것은 화장실 개수(bathrooms)와 침실 개수(bedrooms)입니다. 1행 1열, 2행 2열, 3행 3열은 각 bedrooms, bathrooms, area의 histogram입니다.
이렇듯 간단한 산점도만으로도 독립변수간 상관관계 (다중공선성)을 대략 파악할 수 있습니다.
독립 변수를 drop하지 않고 OLS 회귀 결과를 구해보겠습니다.
df['intercept'] = 1
lm = sm.OLS(df['price'], df[['intercept', 'bedrooms', 'bathrooms', 'area']])
results = lm.fit()
results.summary()
bedrooms의 coef가 -2925.8063입니다. 즉, 침실 개수(bedrooms)와 집 값(price)이 음의 상관 관계를 갖는다는 뜻입니다. bedrooms가 많아질수록 price가 떨어진다는 말입니다. 이전 챕터에서 했던 것 처럼 bedrooms와 price끼리만 OLS 회귀를 해보면 양의 상관 관계를 보입니다. 실제는 양의 상관 관계를 보이는데 여기서는 음의 상관 관계를 보이는 것으로 결과가 잘못 나왔습니다. 이는 위에서 설명한 것처럼 다중공선성으로 인해 회귀 결과가 잘못나온 것입니다.
다중공선성이 있다면 이처럼 회귀 결과를 왜곡합니다. 따라서 회귀를 하기 전에 다중공선성은 반드시 제거해야 합니다.
Scatter plot을 통해 다중공선성을 파악해봤으니 이제 VIF를 통해 다중공선성을 파악해보겠습니다. (Reference3)
y, X = dmatrices('price ~ area + bedrooms + bathrooms', df, return_type = 'dataframe')
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
vif["features"] = X.columns
vif
여기서 X는 6027개의 row를 갖고 아래와 같은 형태입니다. intercept는 기본적으로 들어갑니다.

y도 마찬가지로 6027개의 row를 갖고 아래와 같은 형태입니다.

dmatrices가 원하는 변수만을 matrix 형태로 만들어준 것입니다.
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]이 코드는 행렬 X의 column(여기서는 area, bedrooms, bathrooms)를 순회하면서 해당 column(즉, 변수)의 VIF 값을 계산해줍니다.
최종적으로 아래 결과가 나왔습니다.
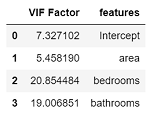
bedrooms와 bathrooms가 10 이상이므로 서로 강한 상관 관계를 보입니다. bedrooms와 bathrooms 중 하나를 drop 하고 회귀를 하면 다중공선성 문제가 해결됩니다. 두 강아지가 서로 싸울 때 한 강아지를 멀찌감치 떼어 놓으면 둘이 싸우지 못합니다. 마찬가지로 다중공선성이 있는 두 변수 중 하나를 제거하면 해당 회귀 모델에서 다중공선성이 없어집니다.
추가로, 해당 변수가 다른 변수와 전혀 상관 관계가 없다면 VIF = 1이고, 해당 변수의 R-squared 값은 0입니다.
VIF 10 이상 변수 drop을 통한 다중공선성 해결 실습
lm = sm.OLS(df['price'], df[['intercept', 'bedrooms', 'area']])
results = lm.fit()
results.summary()
bathrooms 변수를 drop 하고 다시 OLS 회귀를 했습니다. bedrooms의 coef가 1626.8306으로 양수가 되었습니다. 아까는 음수였는데 이제는 양수가 되었습니다. bedrooms의 coefficient는 계수를 의미합니다. 침실 개수(bedsrooms)가 늘어남에 따라 집 값(price)도 높아진다는 뜻입니다. 다중공선성 문제를 해결하니 올바른 결과가 도출되었습니다. 이제 VIF도 다시 구해보겠습니다.
y, X = dmatrices('price ~ area + bedrooms', df, return_type = 'dataframe')
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
vif["features"] = X.columns
vif
모든 VIF가 10미만으로 다중공선성 문제가 해결되었습니다.
추가적으로, R-squared값은 bedrooms를 drop하지 않은 모델과 drop한 모델 모두 0.678입니다. 바로 앞 챕터에서 R-squared의 의미를 알아봤습니다. 결정 계수를 뜻하는 단어로 회귀모형 유용성의 척도입니다. R-squared가 drop 전과 후가 동일하게 0.678이라는 말은 bedrooms와 bathrooms 둘 모두가 필요하지 않다는 뜻입니다. 둘 중 하나만 있어도 된다는 겁니다. bedrooms를 drop했음에도 모델의 예측력에 영향을 끼치지 않았습니다.
References
Reference1 : Variance Inflation Factor (VIF) Explained
Reference3 : statsmodels.stats.outliers_influence.variance_inflation_factor
'데이터 분석' 카테고리의 다른 글
| DATA - 22. 로지스틱 회귀(Logistic Regression) (8) | 2019.05.06 |
|---|---|
| DATA - 21. Higher order term (3) | 2019.05.02 |
| DATA - 19. 가변수(dummy variables)를 활용하여 범주형 데이터 모델링하기 (4) | 2019.04.30 |
| DATA - 18. 다중 선형 회귀 (Multiple linear regression) (4) | 2019.04.30 |
| DATA - 17. 최소자승법(OLS)을 활용한 단순 선형 회귀 (Simple Linear Regression) (8) | 2019.04.28 |




