귀퉁이 서재
DATA - 18. 다중 선형 회귀 (Multiple linear regression) 본문

이전 챕터에서는 단순 선형 회귀 모델에 대해서 배워봤습니다. 단순 선형 회귀식은 아래와 같습니다.
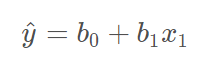
이번 챕터에서는 다중 선형 회귀(Multiple Linear Regression)에 대해 알아보겠습니다. 다중 선형 회귀식은 아래와 같습니다.
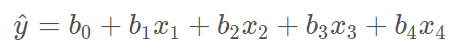
상관 계수(correlation coefficient)는 두 변수 간 선형 관계를 나타내는 척도이기 때문에 단순 선형 회귀에만 쓰이고, 다중 선형 회귀에는 쓰이지 않습니다. 또한, 다중 선형 회귀식에서 양적 데이터 (quantitative) 뿐만 아니라 범주형 데이터 (categorical)도 사용하는 방법을 알아보겠습니다. 아래는 5개의 조건에 따른 집 값을 나타낸 표입니다.
|
종속 변수 |
독립 변수 | ||||
|
집 값 |
지역 | 크기 | 침실 개수 | 화장실 개수 | 집 스타일 |
| $634K | A | 1,600 | 4 | 2 | ranch |
| $120K | B | 3,200 | 7 | 3 | victorian |
| $920K | C | 1,200 | 2 | 2 | ranch |
| $124K | B | 700 | 1 | 1 | lodge |
5개의 독립 변수와, 1개의 종속 변수가 있습니다. 지역, 집 스타일은 범주형 (categorical) 데이터이며, 크기, 침실 개수, 화장실 개수는 양적 (quantitavtive) 데이터입니다. 첫 행만 회귀식으로 표현해보겠습니다.
634 = b₁*A + b₂*1,600 + b₃*4 + b₄*2 + b5*ranch
독립 변수 x에는 항상 숫자만 들어가야 하는데 'A', 'ranch'등 숫자가 아닌 값도 들어 있습니다. 이는 말이 안 되는 식입니다. 범주형 데이터를 숫자로 표현을 해주어야 올바른 식이 됩니다. 이에 대해서는 다음 챕터에서 다루겠습니다.
우선, 범주형 데이터를 제외하고 양적 데이터만을 활용하여 선형 회귀를 해보겠습니다. 크기와 침실 개수, 화장실 개수를 각각 단순 선형 회귀 모델링을 해서 OLS 결과를 도출해 봅시다. (아래는 침실 개수에 대한 코드 예시) 데이터 셋은 제 깃헙에서 다운받을 수 있습니다.
import numpy as np
import pandas as pd
import statsmodels.api as sm;
df = pd.read_csv('house_prices.csv')
df.head()
df['intercept'] = 1
lm_bed = sms.OLS(df['price'], df[['intercept', 'bedrooms']])
results_bed = lm_bed.fit()
results_bed.summary()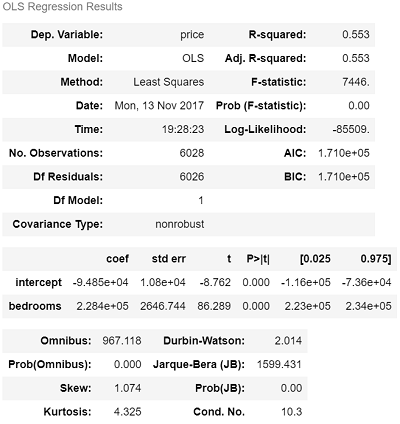
bedrooms 변수의 p-value는 0이기 때문에 통계적으로 유의하다는 결과가 나옵니다. 그리고 계수가 양수기때문에 bedrooms와 price는 양의 상관 관계를 갖습니다. 즉, 침실의 개수가 많아질수록 집값은 비싸진다는 뜻입니다. 동일하게 bathrooms, area에 대해서도 각각 OLS 결과를 도출해봅시다. 세 결과의 R-squared 합은 1보다 큽니다. 이는 크기, 침실 개수, 화장실 개수가 *_서로 독립(independent)이 아니기 때문입니다. *_이제 각각 단순 선형 회귀 모델링을 하는 게 아니라 3개의 변수를 동시에 모델링해보겠습니다.
mlr = sms.OLS(df['price'], df[['intercept', 'area', 'bedrooms', 'bathrooms']])
results_mlr = mlr.fit()
results_mlr.summary()
이 때는 크기(area)에 대한 독립 변수만 p-value가 0이기 때문에 통계적으로 유의하고, 침실 개수(bedrooms)와 화장실 개수(bathrooms)에 대한 독립 변수는 통계적으로 유의하지 않습니다. 그리고 이 때의 R-squared 값은 1보다 작습니다. 또한, bedrooms에 대한 계수가 음수로 바뀌었습니다. 즉, 침실의 개수가 많아질수록 집값이 떨어진다는 뜻입니다. 뭔가 이상합니다. 각각 모델링했을 때와 한번에 모델링 했을 때의 결과가 서로 다릅니다. 이는 나중에 설명할 다중공선성때문입니다. 어쨌건 intercept, bathrooms, bedrooms, area의 계수는 10072, 7345, -2925, 345입니다. area를 예로 들면, area가 1증가할때마다 price가 345증가한다는 뜻입니다.
이제, 선형대수로 다중 선형 회귀의 계수(β)를 구하는 식은 아래와 같습니다. Reference1 전체를 읽을 필요는 없고, 3페이지의 (12)까지만 보시면 아래 공식이 어떻게 유도 되었는지 알 수 있습니다. (Reference1)

X'는 X의 전치행렬(transpose matrix)이고, X-¹은 X의 역행렬(Inverse matrix)입니다. 역행렬을 구하는 방법을 까먹었다면 (Reference2)를 참고하시기 바랍니다. 저도 까먹어서 이 동영상 보며 리마인드했습니다. 물론 직접 역행렬을 구하는 방법을 몰라도 아래 코드를 돌리는데는 전혀 지장이 없습니다.
X = df[['intercept', 'bathrooms', 'bedrooms', 'area']]
y = df['price']
np.dot(np.dot(np.linalg.inv(np.dot(X.transpose(), X)), X.transpose()), y)
>> array([10072.10704671, 7345.3917137 , -2925.80632467, 345.91101884])선형대수로 도출한 계수와 OLS 메서드를 활용하여 도출한 계수가 서로 같은 걸 볼 수 있습니다. 물론, 계수를 선형대수 식으로 직접 구할 일은 없겠지만 원리를 이해하기 위해 가져와 봤습니다.
다중 선형 회귀에서 상관 계수를 구하는 방법에 대해 알아봤습니다. 하지만 bedrooms를 독립 변수로 하고 price를 종속 변수로 하는 단순 선형 회귀에서의 결과와 bedrooms, bathrooms, area를 독립 변수로 하고, price를 종속 변수로 하는 다중 선형 회귀에서의 결과가 서로 상반됐습니다. 또한, 현재는 독립 변수로 양적 데이터만을 사용했습니다. (bedrooms(침실 개수), bathrooms(화자실 개수), area(집 크기)). 하지만, Neighborhood나 Style과 같은 범주형 데이터도 사용을 해야 더 정확하게 집 값을 예측할 수 있습니다. 범주형 데이터를 사용하는 방법에 대해서는 다음 챕터에서 알아보겠습니다.
References
Reference1 : OLS in Matrix Form (NYU)
Reference2 : Youtube (Algebra - Finding the Inverse of a Matrix (1 of 2) A 3X3 Matrix)
'데이터 분석' 카테고리의 다른 글
| DATA - 20. 다중공선성(Multicollinearity)과 VIF(Variance Inflation Factors) (9) | 2019.05.01 |
|---|---|
| DATA - 19. 가변수(dummy variables)를 활용하여 범주형 데이터 모델링하기 (4) | 2019.04.30 |
| DATA - 17. 최소자승법(OLS)을 활용한 단순 선형 회귀 (Simple Linear Regression) (8) | 2019.04.28 |
| DATA - 16. A/B Test (4) | 2019.04.25 |
| DATA - 15. p-value의 함정 (2) | 2019.04.24 |




