- 제가 추천 시스템과 관련된 논문을 작성하고⋯
- 오타 발견해주셔서 고맙습니다. 수정했습니다 :)
- 안녕하세요. 좋은 글 감사합니다 :) 글 중에⋯
- 옙!
- 네~ ^^ 출처만 적어주시면 감사드리겠습니다!
- 안녕하세요 블로그 게시물 잘 보고있습니다.⋯
- 고맙습니다 ^^
- 덕분에 쉽게 이해가 되었습니다. 친절한 설명⋯
- keypoint.pt[0], keypoint.pt[1]이 각각 x, y⋯
- 안녕하세요, ORB알고리즘을 처음 공부하는⋯
- 읽어주셔서 고맙습니다 ~
- 정말 쉽고 흥미로운 이야기들입니다! 잘 읽고⋯
- 아하 그렇군요! ㅎㅎ 포스팅 정말 잘 읽고 갑⋯
- 본 자료는 Udacity에서 참고한 자료라서, 후⋯
- 안녕하세요. 포스팅 너무 잘 봤습니다! 제가⋯
귀퉁이 서재
머신러닝 - 12. 편향(Bias)과 분산(Variance) Trade-off 본문
편향-분산 트레이드오프 (Bias-Variance Trade-off)는 지도 학습(Supervised learning)에서 error를 처리할 때 중요하게 생각해야 하는 요소입니다.
우선, 아래 그림을 통해 편향(Bias)과 분산(Variance)의 관계를 살펴보시기 바랍니다.
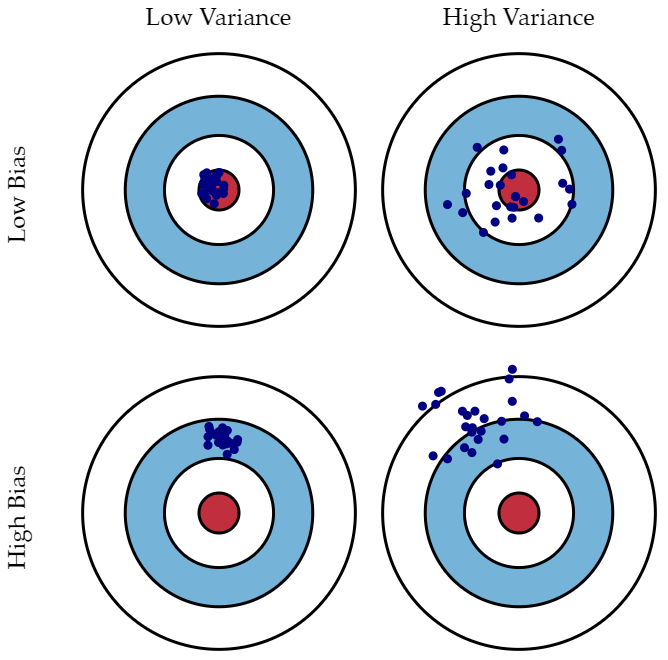
편향은 예측값이 정답과 얼마나 멀리 떨어져 있는지로 측정할 수 있습니다. 분산은 예측값들끼리의 차이로 측정할 수 있습니다.
편향(Bias)
편향은 지나치게 단순한 모델로 인한 error입니다. 편향이 크면 과소 적합(under-fitting)을 야기합니다. 모델에 편향이 크다는 것은 그 모델이 뭔가 중요한 요소를 놓치고 있다는 뜻입니다.
분산(Variance)
분산은 지나치게 복잡한 모델로 인한 error입니다. 훈련 데이터에 지나치게 적합시키려는 모델말입니다. 분산이 크면 과대 적합(Over-fitting)을 야기합니다. 분산이 큰 모델은 훈련 데이터에 지나치게 적합을 시켜 일반화가 되지 않은 모델입니다.
왼쪽은 큰 편향, 작은 분산 (high bias, low variance), 오른쪽은 작은 편향, 큰 분산 (low bias, high variance)를 나타냅니다.
편향은 예측 값과 실제 값의 차이로 나타낼 수 있습니다. 왼쪽 그래프의 예측 값과 실제 값이 차이는 오른쪽 그래프보다 큽니다. 오른쪽 그래프의 예측 값과 실제 값의 차이는 0입니다. 즉 편향이 0이라는 뜻입니다.
분산은 왼쪽 그래프가 더 작습니다. 분산은 주어진 데이터로 학습한 모델이 예측한 값의 변동성을 뜻합니다. 왼쪽 그래프는 일반화가 잘 되어 있기 때문에 예측 값이 일정한 패턴을 나타냅니다. 반면, 오른쪽 그래프는 들쑥날쑥 합니다. 예측 값이 일정한 패턴이 없다는 뜻입니다. 즉, 분산이 크다는 뜻입니다. 따라서 왼쪽 그래프는 분산이 작고, 오른쪽 그래프는 분산이 큽니다.
편향-분산 Trade-off
Error를 구하는 공식은 아래와 같습니다.
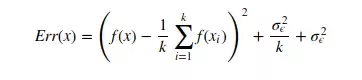
첫번째 term: 편향의 제곱
두 번째 term: 분산
세 번째 term: 줄일 수 없는 불가피한 error (irreducible error)
마지막 error는 일상생활에서 발생할 수 있는 불가피한 error를 뜻합니다. 전체 모델의 error는 이렇게 편향, 분산, 불가피한 error를 모두 합한 것과 같습니다. 하지만 편향과 분산 간에는 trade-off 관계가 있습니다.
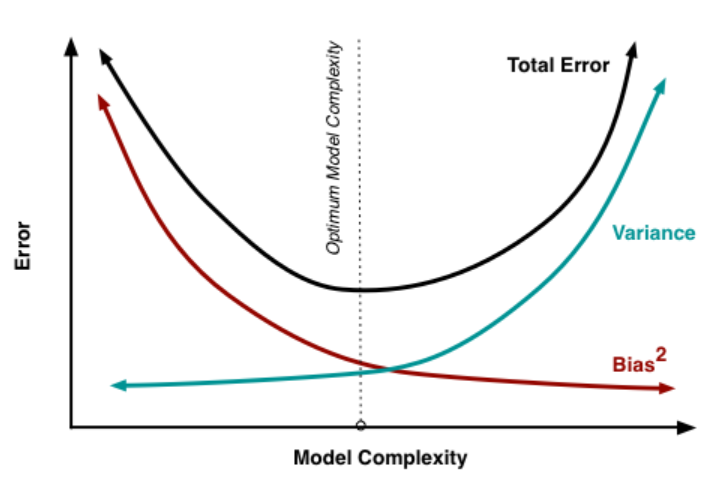
모델이 복잡해질 수록 편향은 작아지고, 분산은 커집니다. 즉 over-fitting 됩니다. 모델이 단순해질수록 편향은 커지고, 분산은 작아집니다. 즉, under-fitting 됩니다. 무조건 편향만 줄일 수도, 무조건 분산만 줄일 수도 없습니다. 오류를 최소화하려면 편향과 분산의 합이 최소가 되는 적당한 지점을 찾아야 합니다.
References
Reference1: Quora (What is the best way to explain the bias-variance trade-off in layman's terms?)
Reference2: StatQuest with Josh Starmer (Machine Learning Fundamentals: Bias and Variance)
Reference3: SlideShare (boostring 기법 이해 (bagging vs boosting))
'머신러닝' 카테고리의 다른 글
| 머신러닝 - 14. 에이다 부스트(AdaBoost) (14) | 2019.10.04 |
|---|---|
| 머신러닝 - 13. 파라미터(Parameter)와 하이퍼 파라미터(Hyper parameter) (12) | 2019.09.27 |
| 머신러닝 - 12. 편향(Bias)과 분산(Variance) Trade-off (0) | 2019.09.13 |
| 머신러닝 - 11. 앙상블 학습 (Ensemble Learning): 배깅(Bagging)과 부스팅(Boosting) (8) | 2019.09.12 |
| 머신러닝 - 10. 교차검증(Cross Validation)과 혼동행렬(Confusion Matrix) (0) | 2019.08.13 |
| 머신러닝 - 9. 차원 축소와 PCA (Principal Components Analysis) (9) | 2019.08.11 |
- Tag
- bias, Bias Variance, Bias-Variance Trade-off, Variance, 분산, 편향, 편향-분산 트레이드오프, 편향과 분산
