귀퉁이 서재
OpenCV - 15. 리매핑(Remapping), 오목/볼록 렌즈 왜곡(Lens Distortion), 방사 왜곡(Radial Distortion) 본문
OpenCV - 15. 리매핑(Remapping), 오목/볼록 렌즈 왜곡(Lens Distortion), 방사 왜곡(Radial Distortion)
Baek Kyun Shin 2020. 10. 2. 12:57
이번 포스팅에서는 렌즈를 왜곡하는 방법에 대해 알아보겠습니다. 이번 포스팅 역시 '파이썬으로 만드는 OpenCV 프로젝트(이세우 저)'를 정리한 것임을 밝힙니다.
코드: github.com/BaekKyunShin/OpenCV_Project_Python/tree/master/05.geometric_transform
렌즈 왜곡(Lens Distortion)
지금까지 이미지 이동(Translation), 확대/축소(Scaling), 회전(Rotation), 어핀 변환(Affine Transformation), 원근 변환(Perspective Transformation)에 대해 배웠습니다. 이는 모두 변환 행렬을 이용해서 구할 수 있습니다. 하지만 변환 행렬로는 구할 수 없는 모양의 변환도 있습니다. 렌즈 왜곡 변환이 바로 변환 행렬로는 구할 수 없는 변환입니다. 렌즈 왜곡 변환에는 리매핑, 오목 렌즈/볼록 렌즈 왜곡, 방사 왜곡이 있습니다. 차례대로 살펴보겠습니다.
리매핑(Remapping)
리매핑이란 규칙성 없이 마음대로 이미지의 모양을 변환하는 것을 말합니다. 리매핑을 위해 OpenCV는 cv2.remap()이라는 함수를 제공합니다.
- dst = cv2.remap(src, mapx, mapy, interpolation, dst, borderMode, borderValue)
src: 입력 이미지
mapx, mapy: x축과 y축으로 이동할 좌표, src와 동일한 크기, dtype=float32
dst(optional): 결과 이미지
나머지 인자는 cv2.warpAffine()과 동일
예를 들어, mapx[0][0]=10, mapy[0][0]=5로 지정했다면 이 의미는 src 좌표 (0, 0)에 있는 픽셀을 (10, 5)로 옮기라는 것입니다. mapx와 mapy는 초기 값으로 0 같은 의미 없는 값이 아니라 원래 이미지의 좌표 값을 갖는 것이 좋습니다. 왜냐하면 전체 픽셀 중 옮기고 싶은 픽셀에 대해서만 새로운 좌표를 지정하거나 원래 위치에서 얼마만큼 이동하라고 명령하는 것이 편하기 때문입니다. mapx와 mapy를 np.zeros()로 초기화한 뒤 for문으로 초기화할 수 있지만 이렇게 하면 시간이 너무 오래 걸립니다. 대신 다음과 같이 np.indices() 함수를 쓰면 빠르게 초기화할 수 있습니다.
mapy, mapx = np.indices( (rows, cols), dtype=np.float32)아래는 np.indices() 함수의 예시입니다. 반환된 결과의 0번째가 행 배열, 1번째가 열 배열입니다.
>>> np.indices((2,2))
array([[[0, 0],
[1, 1]],
[[0, 1],
[0, 1]]])
>>> np.indices((3, 3))
array([[[0, 0, 0],
[1, 1, 1],
[2, 2, 2]],
[[0, 1, 2],
[0, 1, 2],
[0, 1, 2]]])아래는 이미지를 뒤집는 코드입니다. 변환 행렬과 cv2.remap() 함수로 각각 구현해서 똑같은 결과를 보여줄 겁니다. 참고로 영상을 뒤집기 위한 연산식은 다음과 같습니다. 이 연산식을 활용하여 변환 행렬을 구할 것입니다.
x' = cols - x - 1
y' = rows - y - 1
# 변환행렬과 리매핑으로 이미지 뒤집기 (remap_flip.py)
import cv2
import numpy as np
import time
img = cv2.imread('../img/yeosu_small.jpg')
rows, cols = img.shape[:2]
# 뒤집기 변환 행렬로 구현 ---①
st = time.time()
mflip = np.float32([ [-1, 0, cols-1],[0, -1, rows-1]]) # 변환 행렬 생성
fliped1 = cv2.warpAffine(img, mflip, (cols, rows)) # 변환 적용
print('matrix:', time.time()-st)
# remap 함수로 뒤집기 구현 ---②
st2 = time.time()
mapy, mapx = np.indices((rows, cols),dtype=np.float32) # 매핑 배열 초기화 생성
mapx = cols - mapx -1 # x축 좌표 뒤집기 연산
mapy = rows - mapy -1 # y축 좌표 뒤집기 연산
fliped2 = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR) # remap 적용
print('remap:', time.time()-st2)
# 결과 출력 ---③
cv2.imshow('origin', img)
cv2.imshow('fliped1',fliped1)
cv2.imshow('fliped2',fliped2)
cv2.waitKey()
cv2.destroyAllWindows()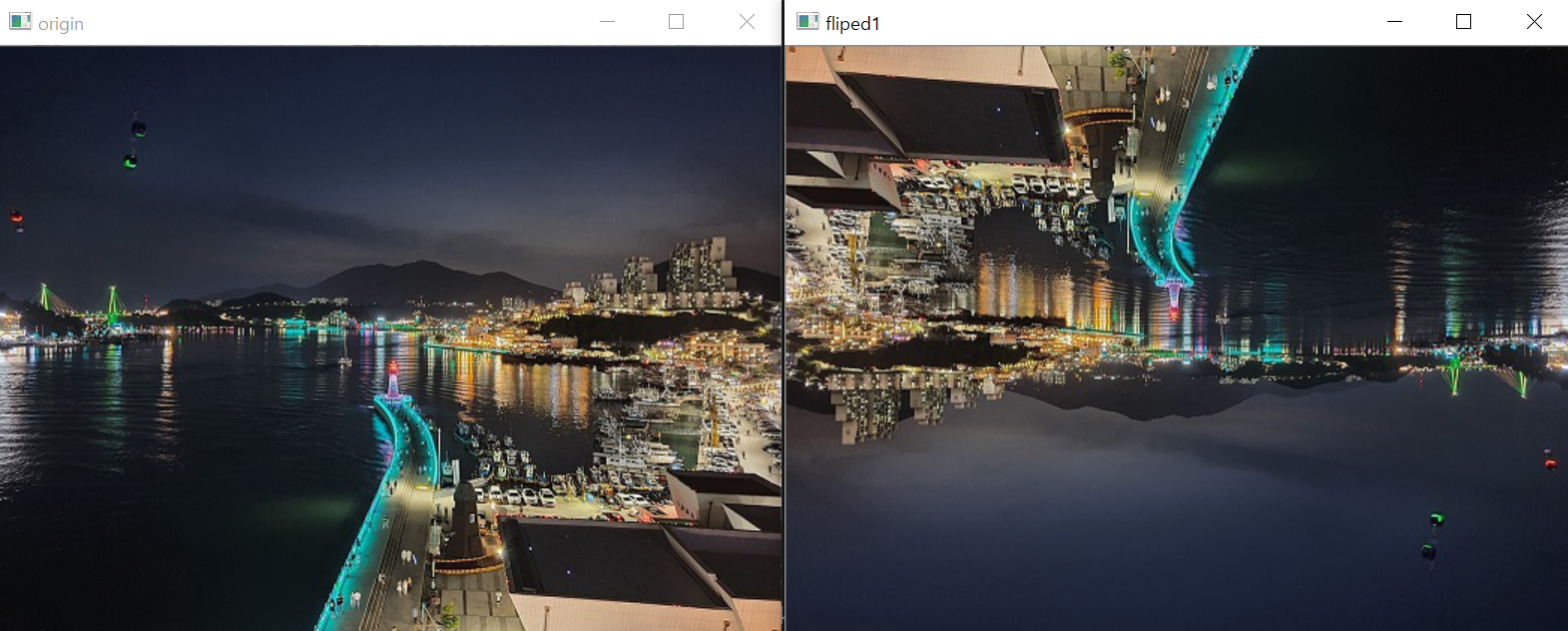
변환행렬을 이용하여 뒤집은 이미지와 cv2.remap() 함수로 리매핑하여 뒤집은 이미지의 결과는 똑같습니다. (공간 관계상 뒤집힌 배경 이미지는 하나만 삽입했습니다.) 표현만 다를 뿐이지 그 의미는 같습니다. 그러나 cv2.remap() 함수로 변환하는 것은 변환 행렬로 변환하는 것보다 수행 속도가 더 느립니다. 따라서 변환행렬로 표현할 수 있는 것은 변환행렬로 변환을 하는 것이 좋습니다. 변환행렬로 표현할 수 없는 비선형 변환에만 cv2.remap() 함수를 사용하는 것이 좋습니다.
삼각함수를 이용한 비선형 리매핑
변환 행렬로 표현할 수 없는 비선형 변환을 cv2.remap() 함수로 구현해보겠습니다.
# 삼각함수를 이용한 비선형 리매핑 (remap_sin_cos.py)
import cv2
import numpy as np
l = 20 # 파장(wave length)
amp = 15 # 진폭(amplitude)
img = cv2.imread('../img/taekwonv1.jpg')
rows, cols = img.shape[:2]
# 초기 매핑 배열 생성 ---①
mapy, mapx = np.indices((rows, cols),dtype=np.float32)
# sin, cos 함수를 적용한 변형 매핑 연산 ---②
sinx = mapx + amp * np.sin(mapy/l)
cosy = mapy + amp * np.cos(mapx/l)
# 영상 매핑 ---③
img_sinx=cv2.remap(img, sinx, mapy, cv2.INTER_LINEAR) # x축만 sin 곡선 적용
img_cosy=cv2.remap(img, mapx, cosy, cv2.INTER_LINEAR) # y축만 cos 곡선 적용
# x,y 축 모두 sin, cos 곡선 적용 및 외곽 영역 보정
img_both=cv2.remap(img, sinx, cosy, cv2.INTER_LINEAR, \
None, cv2.BORDER_REPLICATE)
# 결과 출력
cv2.imshow('origin', img)
cv2.imshow('sin x', img_sinx)
cv2.imshow('cos y', img_cosy)
cv2.imshow('sin cos', img_both)
cv2.waitKey()
cv2.destroyAllWindows()
x좌표, y좌표에 sin, cos 함수를 적용하여 새로운 사인파 코사인파 곡선으로 왜곡된 이미지를 만들어 주었습니다. 마지막 이미지에는 sin, cos 함수를 모두 적용하였는데, cv2.BORDER_REPLICATE 파라미터로 외곽 보정까지 해주어 외곽의 사라진 영역이 보정된 것을 볼 수 있습니다.
오목 렌즈와 볼록 렌즈 왜곡
오목 렌즈, 볼록 렌즈 왜곡에 대해서 살펴보기 전에 직교 좌표계, 극좌표계에 대해 먼저 알아보겠습니다. 우선, 아래 그림을 보겠습니다.
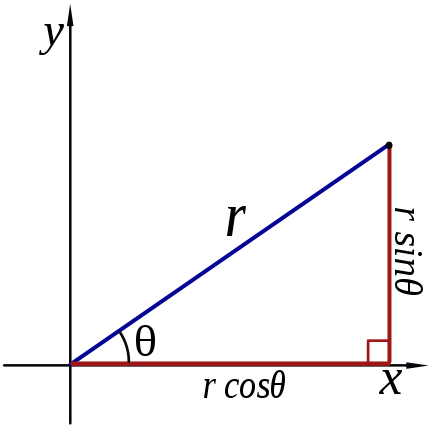
우리는 일반적으로 x축과 y축의 직각으로 각각 선을 그어서 만나는 지점을 좌표 (x, y)로 나타냅니다. 이러한 형태의 좌표 시스템을 직교 좌표계(Cartesian coordinate system)라고 부릅니다. 반면, 원점으로부터의 거리(r)와 사잇각(Θ)을 이용해서 (r, Θ)로 나타내는 방법이 있는데, 이를 극좌표계(Polar coordinate system)라고 부릅니다. 두 좌표계는 상호 변환이 가능합니다. 좌표 변환은 연산식을 이용해도 되지만, OpenCV는 좌표 변환을 위해 다음과 같은 함수를 제공합니다.
r, theta = cv2.cartToPolar(x, y): 직교 좌표 → 극좌표 변환
x, y = cv2.polarToCart(r, theta): 극좌표 → 직교 좌표 변환
좌표의 변환뿐만 아니라 좌표의 기준점 변환도 중요합니다. 일반적으로 직교 좌표계를 사용할 때는 좌측 상단을 원점(0, 0)으로 정합니다. 그러나 극좌표에서는 이미지의 중앙을 원점으로 해야 합니다. 이미지의 중앙을 (0, 0)으로 두기 위해서 좌표의 값을 -1 ~ 1로 정규화해야 합니다.
# 볼록/오몬 렌즈 왜곡 효과 (remap_lens.py)
import cv2
import numpy as np
img = cv2.imread('../img/taekwonv1.jpg')
print(img.shape)
rows, cols = img.shape[:2]
# ---① 설정 값 셋팅
exp = 2 # 볼록, 오목 지수 (오목 : 0.1 ~ 1, 볼록 : 1.1~)
scale = 1 # 변환 영역 크기 (0 ~ 1)
# 매핑 배열 생성 ---②
mapy, mapx = np.indices((rows, cols),dtype=np.float32)
# 좌상단 기준좌표에서 -1~1로 정규화된 중심점 기준 좌표로 변경 ---③
mapx = 2*mapx/(cols-1)-1
mapy = 2*mapy/(rows-1)-1
# 직교좌표를 극 좌표로 변환 ---④
r, theta = cv2.cartToPolar(mapx, mapy)
# 왜곡 영역만 중심확대/축소 지수 적용 ---⑤
r[r< scale] = r[r<scale] **exp
# 극 좌표를 직교좌표로 변환 ---⑥
mapx, mapy = cv2.polarToCart(r, theta)
# 중심점 기준에서 좌상단 기준으로 변경 ---⑦
mapx = ((mapx + 1)*cols-1)/2
mapy = ((mapy + 1)*rows-1)/2
# 재매핑 변환
distorted = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)
cv2.imshow('origin', img)
cv2.imshow('distorted', distorted)
cv2.waitKey()
cv2.destroyAllWindows()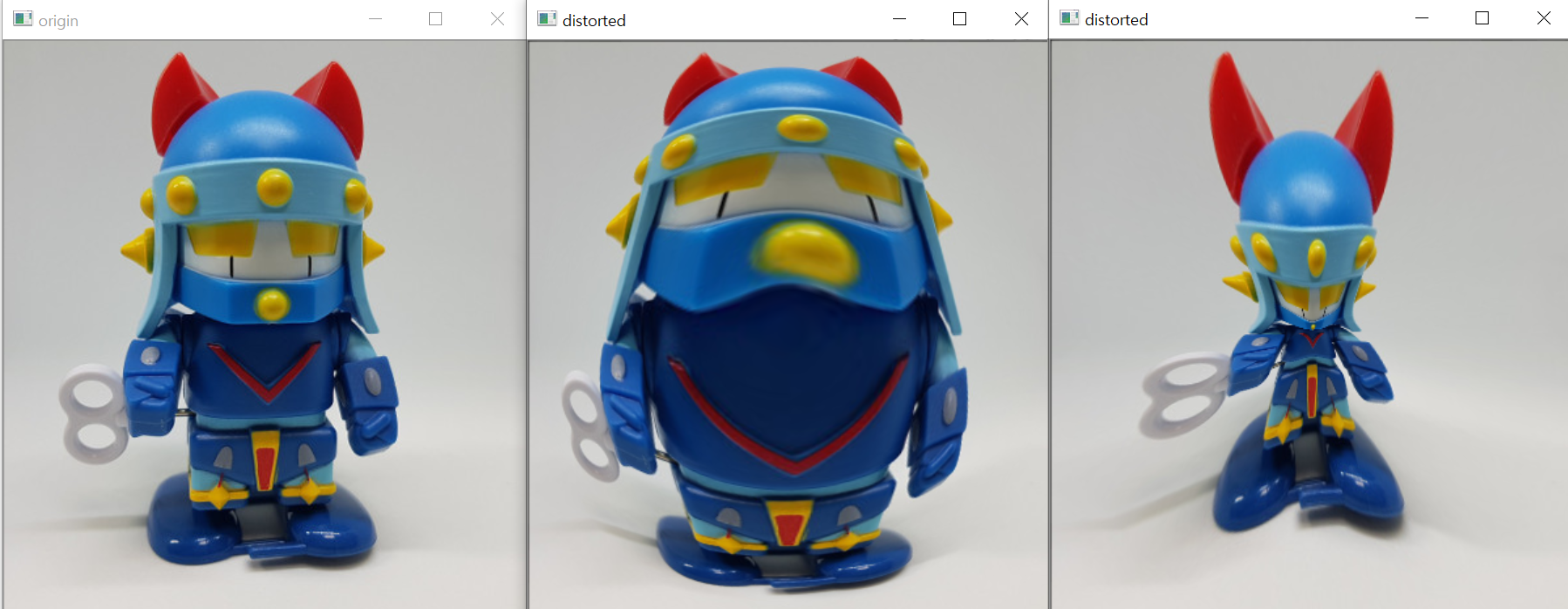
exp는 이미지의 왜곡 지수를 나타내는 변수로 1이면 원본과 동일하게 하고, 1보다 작으면 오목 렌즈 효과를 내고, 1보다 크면 볼록 렌즈 효과를 냅니다. 맨 오른쪽은 exp=0.5로 설정한 결과입니다. scale은 이미지에서 렌즈 효과를 주고 싶은 원 모양 영역의 크기를 비율로 나타낸 것입니다. scale=1은 100%를 의미합니다.
그리고 아래 코드는 좌표의 기준점을 바꾸고 -1~1 범위로 정규화하는 기능을 합니다. 이는 이후에 다시 좌상단 기준점으로 변경됩니다.
mapx = 2*mapx/(cols-1)-1
mapy = 2*mapy/(rows-1)-1실질적인 렌즈 효과는 아래 코드에서 이루어집니다.
r[r< scale] = r[r<scale] **exp 앞서 좌표의 범위를 -1~1로 정규화했습니다. 따라서 scale의 최댓값은 1입니다. 1을 넘는 값을 가질 수는 없습니다. 극좌표계로 바꿨을 때의 r은 원의 반지름입니다. 반지름이 scale보다 작은 범위에 있는 좌표에 대해서는 exp(왜곡 지수)를 곱해주었습니다. 이때 왜곡 지수가 1보다 크면 볼록 렌즈 효과를, 1보다 작으면 오목 렌즈 효과를 줍니다.
방사 왜곡
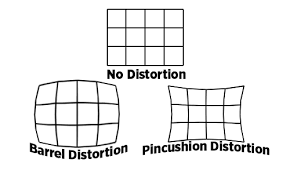
카메라를 통해 이미지를 촬영할 때 카메라 가장자리 부분에서 약간의 왜곡이 생기는 것을 본 적이 있을 겁니다. 이런 현상을 배럴 왜곡(barrel distortiaon)이라고 합니다.
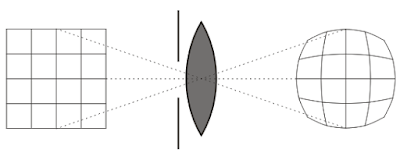
위 그림과 같이 실제 이미지를 렌즈를 통해 촬영하면 가장자리 부분이 약간 둥그스름해지는 것입니다. 둥근 모양이 배럴 통 같다고 하여 배럴 왜곡이라고 합니다. 반면, 가장자리 부분이 안쪽으로 들어가는 형태의 왜곡을 핀쿠션 왜곡(pinsushion distortion)이라고 합니다.
배럴 왜곡과 핀쿠션 왜곡을 구현해보겠습니다.
# 배럴 왜곡, 핀쿠션 왜곡 (reamp_barrel.py)
import cv2
import numpy as np
# 왜곡 계수 설정 ---①
k1, k2, k3 = 0.5, 0.2, 0.0 # 배럴 왜곡
#k1, k2, k3 = -0.3, 0, 0 # 핀큐션 왜곡
img = cv2.imread('../img/girl.jpg')
rows, cols = img.shape[:2]
# 매핑 배열 생성 ---②
mapy, mapx = np.indices((rows, cols),dtype=np.float32)
# 중앙점 좌표로 -1~1 정규화 및 극좌표 변환 ---③
mapx = 2*mapx/(cols-1)-1
mapy = 2*mapy/(rows-1)-1
r, theta = cv2.cartToPolar(mapx, mapy)
# 방사 왜곡 변영 연산 ---④
ru = r*(1+k1*(r**2) + k2*(r**4) + k3*(r**6))
# 직교좌표 및 좌상단 기준으로 복원 ---⑤
mapx, mapy = cv2.polarToCart(ru, theta)
mapx = ((mapx + 1)*cols-1)/2
mapy = ((mapy + 1)*rows-1)/2
# 리매핑 ---⑥
distored = cv2.remap(img,mapx,mapy,cv2.INTER_LINEAR)
cv2.imshow('original', img)
cv2.imshow('distorted', distored)
cv2.waitKey()
cv2.destroyAllWindows()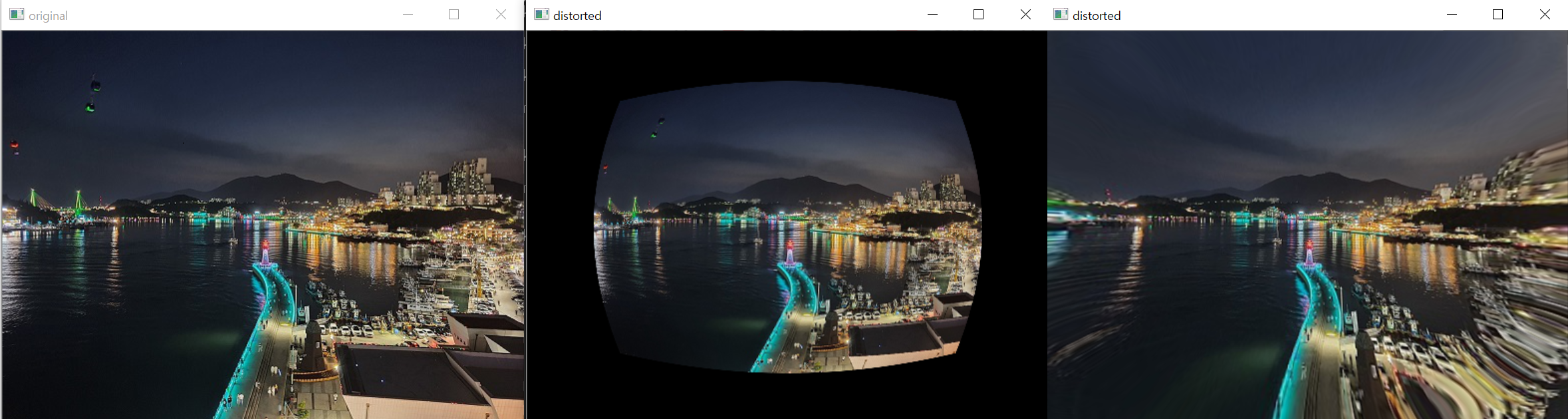
코드의 아래 부분만 제외하고는 오목 렌즈, 볼록 렌즈 왜곡과 전체적인 프로세스는 비슷합니다.
ru = r*(1+k1*(r**2) + k2*(r**4) + k3*(r**6))
위 연산식은 배럴 왜곡, 핀쿠션 왜곡을 적용해주는 연산식입니다. k1, k2, k3 값에 따라 배럴 왜곡이 될 수도 있고 핀쿠션 왜곡이 될 수도 있습니다. 왜곡 계수 설정하는 코드에서 주석을 서로 바꿔가며 실행해보시기 바랍니다.
'OpenCV' 카테고리의 다른 글
| OpenCV - 17. 필터(Filter)와 컨볼루션(Convolution) 연산, 평균 블러링, 가우시안 블러링, 미디언 블러링, 바이레터럴 필터 (2) | 2020.10.05 |
|---|---|
| OpenCV - 16. 모자이크 처리(Mosaic), 리퀴파이(Liquify), 왜곡 거울(Distortion Mirror) (2) | 2020.10.04 |
| OpenCV - 14. 이미지 뒤틀기(어핀 변환, 원근 변환) (6) | 2020.09.29 |
| OpenCV - 13. 이미지 이동(Translation), 확대/축소(Scaling), 회전(Rotation) (0) | 2020.09.28 |
| OpenCV - 12. 이미지 유사도 비교, 사람 얼굴과 해골 합성, 모션 감지 CCTV (2) | 2020.09.24 |




