귀퉁이 서재
머신러닝 - 9. 차원 축소와 PCA (Principal Components Analysis) 본문

차원 축소와 PCA
차원 축소는 많은 feature로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것입니다. 일반적으로 차원이 증가할수록, 즉 feature가 많아질수록 예측 신뢰도가 떨어지고, 과적합(overfitting)이 발생하고, 개별 feature간의 상관관계가 높을 가능성이 있습니다.
PCA(주성분 분석, Principal Component Analysis)는 고차원의 데이터를 저차원의 데이터로 축소시키는 차원 축소 방법 중 하나입니다. (Reference1) 머신러닝을 할 때 훈련 데이터의 feature가 많은 경우가 있습니다. 하지만 모든 feature가 결과에 주요한 영향을 끼치는 것은 아닙니다. 가장 중요한 feature가 있을 것이고, 그다음 중요한 feature가 있을 것이고.. 가장 쓸모없는 feature도 있을 겁니다. 이런 feature 중 가장 중요한 feature 몇 개 만을 선택하는 게 PCA입니다. 10개의 feature가 있다고 해봅시다. 10개의 feature와 1개의 label을 매핑시키는 그래프를 그리려면 10차원의 그래프가 있어야 합니다. 3차원이 넘어가면 우리의 눈으로는 볼 수 없겠죠. 이때 중요한 2개의 feature만 선택해서 그래프를 그린다고 합시다. 그러면 2차원의 그래프가 될 것입니다. '10개의 feature 중 2개의 feature만 뽑아서 분석하겠다, 즉 10차원은 2차원으로 축소시키겠다.'라는 의미로 PCA는 차원축소 방법 중 하나인 것입니다.
차원 축소를 하는 이유
그러면 왜 차원 축소(Demensianlity Reduction)를 할까요?
1. 시각화 (Visualization)
위에서 설명한 것처럼 3차원이 넘어간 시각화는 우리 눈으로 볼 수 없습니다. 따라서 차원 축소를 통해 시각화를 할 수 있습니다. 시각화를 통해 데이터 패턴을 쉽게 인지할 수 있습니다.
2. 노이즈 제거 (Reduce Noise)
쓸모없는 feature를 제거함으로써 노이즈를 제거할 수 있습니다.
3. 메모리 절약 (Preserve useful info in low memory)
쓸모없는 feature를 제거하면 메모리도 절약이 되겠죠.
4. 퍼포먼스 향상
불필요한 feature들을 제거해 모델 성능 향상에 기여를 합니다.
차원의 시각화
PCA 동작 원리 및 프로세스에 대한 설명 및 그림은 모두 StatQuest 유튜브에서 가져온 것입니다. (Reference2)
아래는 총 6명의 학생의 국어 성적입니다. feature가 1개(국어)이므로 1차원(선형)으로 시각화를 할 수 있습니다.
| 학생1 | 학생2 | 학생3 | 학생4 | 학생5 | 학생6 | |
| 국어 | 10 | 11 | 8 | 3 | 2 | 1 |

보시는 바와 같이 학생 1, 2, 3은 높은 점수대에 위치해 있고, 학생 4, 5, 6은 낮은 점수대에 위치해 있습니다. 학생 1, 2, 3과 학생 4, 5, 6을 서로 그루핑 할 수 있습니다. 이제 국어, 영어 성적으로 확대해보겠습니다.
| 학생1 | 학생2 | 학생3 | 학생4 | 학생5 | 학생6 | |
| 국어 | 10 | 11 | 8 | 3 | 2 | 1 |
| 영어 | 6 | 4 | 5 | 3 | 2.8 | 1 |

feature가 2개이므로 2차원 그래프입니다. x축은 국어, y축은 영어입니다. 역시 학생 1, 2, 3과 학생 4, 5, 6을 서로 그루핑할 수 있습니다. 차원을 하나 더 늘려보겠습니다.
| 학생1 | 학생2 | 학생3 | 학생4 | 학생5 | 학생6 | |
| 국어 | 10 | 11 | 8 | 3 | 2 | 1 |
| 영어 | 6 | 4 | 5 | 3 | 2.8 | 1 |
| 수학 | 12 | 9 | 10 | 2.5 | 1.3 | 2 |

수학이라는 feature가 하나 더 늘었기 때문에 3차원 그래프가 되었습니다. 차원을 하나 더 늘려볼까요?
| 학생1 | 학생2 | 학생3 | 학생4 | 학생5 | 학생6 | |
| 국어 | 10 | 11 | 8 | 3 | 2 | 1 |
| 영어 | 6 | 4 | 5 | 3 | 2.8 | 1 |
| 수학 | 12 | 9 | 10 | 2.5 | 1.3 | 2 |
| 과학 | 5 | 7 | 6 | 2 | 4 | 7 |
안타깝게도 4차원 그래프는 그릴 수 없습니다. 우리의 눈은 3차원까지 밖에 볼 수 없으므로 4차원 그래프는 그릴 수도 볼 수도 없습니다. 따라서 feature가 4개 이상 일 때는 시각화를 할 수 없습니다. 이를 해결하기 위한 방법이 PCA입니다.
PCA 프로세스
2차원 그래프를 토대로 PCA 프로세스를 설명해보겠습니다.
| 학생1 | 학생2 | 학생3 | 학생4 | 학생5 | 학생6 | |
| 국어 | 10 | 11 | 8 | 3 | 2 | 1 |
| 영어 | 6 | 4 | 5 | 3 | 2.8 | 1 |

1. 데이터의 중심 정하기

x축의 중심, y축의 중심(빨간 X)을 각각 구한 뒤 6개의 데이터의 중심(파란 X)을 구합니다.
2. 데이터의 중심을 원점(0, 0)으로 이동하기
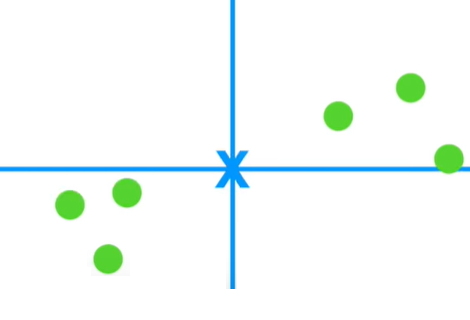
데이터의 중심을 원점(0, 0)으로 이동시킵니다. 데이터를 이동하더라도 데이터 간 상대 위치에는 변함이 없습니다.
3. 원점을 지나는 직선 그리기 (Random 하게)

4. 주어진 데이터에 가장 fit 하도록 원점을 지나는 직선을 회전
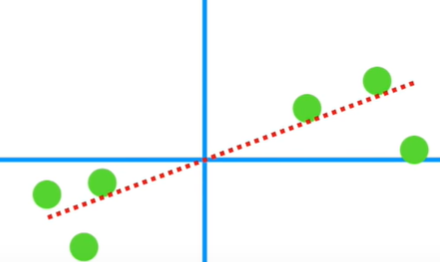
이 직선은 6개의 데이터에 가장 fit 한 직선입니다.
여기서 잠깐! 직선이 데이터에 fit 하다는 것은 어떻게 판단할까요?
데이터를 직선에 수직이 되게 사상(projection)시킵니다. 그런 다음 원점부터 사상된 점까지의 거리를 구합니다. 그 거리가 바로 아래의 d₁입니다. 원점으로부터 6개 모든 사상된 점까지의 거리 합이 최대가 되게 하면 됩니다. 그러면 해당 직선이 데이터에 가장 fit 해집니다. 왜 이 거리가 최대가 되면 가장 fit 해지는지 알아보겠습니다.

피타고라스의 정리에 의해 a² = b² + c²입니다. 데이터는 고정되어 있는 상태에서 직선을 회전시켜야 합니다. 그 말은 a는 동일하게 유지가 되고 c와 b가 바뀐다는 뜻입니다.
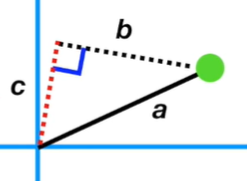
아래와 같이 직선이 데이터 쪽으로 더 fit 해질수록 c는 커지고 b는 작아집니다.

따라서 직선이 데이터에 fit 해지려면 c가 최대가 되어야 한다는 뜻입니다. c는 원점으로부터 데이터를 직선으로 사상한 점까지의 거리입니다. 모든 데이터의 c값의 합이 최대가 되면 직선은 데이터에 가장 fit 해지게 됩니다.
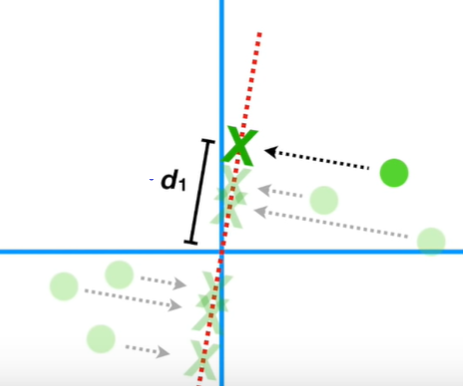

원점으로부터 6개의 사상된 점과의 거리의 제곱의 합을 sum of squared (SS)라고 합니다. 이 SS가 최대가 되면 직선이 데이터에 fit 해집니다. SS가 최대라는 것은 variance가 최대일 때를 뜻합니다. variance가 최대가 되어야 정보의 손실을 최소화할 수 있습니다.

이 직선이 SS가 가장 최대일 때이며, 데이터에 가장 fit 한 직선입니다. 이 직선을 Principal Component 1 (PC1)이라고 합니다. Principal Component 1을 해석하면 주성분 1입니다. 이 6개의 데이터를 설명하는 가장 중요한 성분이라는 뜻입니다. PC1의 기울기는 0.25입니다. x(국어)가 4만큼 이동할 때 y(영어)는 1만큼 이동한다는 뜻입니다. 데이터는 거의 x(국어) 축을 따라 퍼져있고, y(영어) 축을 따라서는 조금만 퍼져있습니다. 국어 4에 영어 1을 믹스해놓은 것이 PC1입니다. 이렇듯 feature1과 feature2를 믹스해놓은 것을 선형 결합 (Linear Combination)이라고 합니다. 다시 정리하자면 feature1 4만큼과 feature2 1만큼을 선형결합한 PC1이 해당 데이터를 가장 잘 설명하는 요소라는 것입니다.

5. 스케일링을 통해 EigenVector 만들기
피타고라스의 정리에 의해 x가 4이고, y가 1이면 빨간 빗변은 4.12입니다. 4.12를 1로 스케일링해주어야 합니다.
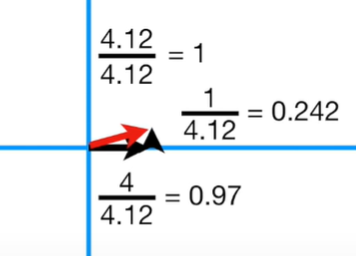
스케일링 결과, 0.97만큼의 feature1, 0.242만큼의 feature2를 믹스하면 1만큼의 unit vector가 나옵니다. 이때 빨간색의 크기 1인 unit vector를 PC1의 "Singular Vector" 혹은 "Eigenvector"라 합니다. 그리고 feature1 0.97, feature2 0.242의 조합을 "Loading Scores"라고 합니다. 이는 feature1이 feature2보다 4배 중요하다는 뜻입니다.

또한, PC1의 SS를 Eigenvalue for PC1이라고 합니다.
6. PC2도 동일한 프로세스로 진행
이제 PC2를 알아봅시다. PC2는 간단합니다. 원점을 지나며 PC1에 수직인 직선을 그려주면 됩니다. PC1의 기울기가 0.25였으므로 PC2의 기울기는 -4가 될 것입니다. (서로 수직인 기울기의 곱은 -1이므로)

PC1과 마찬가지로 스케일링을 먼저 해줍니다. 그럼 PC2의 Loading scores을 구할 수 있습니다. 계산을 하면 Loading scores for PC2는 feature1 -0.242, feature2 0.97입니다. 이 말은 PC1과는 다르게 PC2에서는 feature2가 feature1보다 4배 더 중요하다는 뜻입니다. 드디어 PC1과 PC2를 모두 구했습니다.
PC1과 PC2에 대해서 사상(Projection)시킨 점은 아래와 같습니다.

7. PC축 회전
PC1이 x축에 수평이 되게 데이터를 아래와 같이 회전합니다.

8. 데이터 복원
그다음 원 데이터를 구하기 위해 사상된 점을 활용합니다. 아래와 같이 말이죠.

6개의 모든 점에 대해서 동일하게 진행합니다.

PCA가 모두 끝났습니다.
Variation
이제, PC1, PC2가 해당 데이터를 얼마나 설명하느냐를 알아봐야겠죠? SS를 n-1로 나누어 Variation을 구할 수 있습니다. PC1의 Variation이 15, PC2의 Variation이 3이라 할 때 전체 Variation은 18입니다. PC1은 15/18 = 0.83 = 83%만큼 데이터를 설명합니다. 그 말은 PC1이 83%만큼 중요하다는 뜻입니다.

PC2의 Variation은 자연히 17%겠죠. 각 PC의 Variation에 대한 그래프를 Scree Plot이라고 합니다.

그렇다면 feature가 4개인 경우에 어떻게 되는지 보겠습니다. 앞서 말씀드린 것처럼 feature가 4개일 때 4차원 시각화는 할 수 없습니다. Scree Plot을 그렸을 때 아래와 같이 나온다고 합시다. PC1, PC2가 90% 이상을 차지합니다. 따라서 PC1과 PC2 만으로 2차원 시각화를 하더라도 전체의 90% 이상을 설명할 수 있습니다.

실습
sklearn을 활용한 PCA 실습 코드는 제 깃헙에서 보실 수 있습니다.
import pandas as pd
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn import decomposition
# Eating, exercise habbit and their body shape
df = pd.DataFrame(columns=['calory', 'breakfast', 'lunch', 'dinner', 'exercise', 'body_shape'])
df.loc[0] = [1200, 1, 0, 0, 2, 'Skinny']
df.loc[1] = [2800, 1, 1, 1, 1, 'Normal']
df.loc[2] = [3500, 2, 2, 1, 0, 'Fat']
df.loc[3] = [1400, 0, 1, 0, 3, 'Skinny']
df.loc[4] = [5000, 2, 2, 2, 0, 'Fat']
df.loc[5] = [1300, 0, 0, 1, 2, 'Skinny']
df.loc[6] = [3000, 1, 0, 1, 1, 'Normal']
df.loc[7] = [4000, 2, 2, 2, 0, 'Fat']
df.loc[8] = [2600, 0, 2, 0, 0, 'Normal']
df.loc[9] = [3000, 1, 2, 1, 1, 'Fat']
# X is feature vectors
X = df[['calory', 'breakfast', 'lunch', 'dinner', 'exercise']]
# Y is labels
Y = df[['body_shape']]
x_std = StandardScaler().fit_transform(X)
pca = decomposition.PCA(n_components=1)
sklearn_pca_x = pca.fit_transform(x_std)
sklearn_result = pd.DataFrame(sklearn_pca_x, columns=['PC1'])
sklearn_result['y-axis'] = 0.0
sklearn_result['label'] = Y
sns.lmplot('PC1', 'y-axis', data=sklearn_result, fit_reg=False,
scatter_kws={"s":50}, hue='label');
References
Referecne1: wikipedia (주성분 분석)
Reference2: SataQuest: Principal Component Analysis (PCA), Step-by-Step
Reference3: [머신러닝] PCA 차원 축소 알고리즘 및 파이썬 구현 (주성분 분석)
'머신러닝' 카테고리의 다른 글
| 머신러닝 - 11. 앙상블 학습 (Ensemble Learning): 배깅(Bagging)과 부스팅(Boosting) (12) | 2019.09.12 |
|---|---|
| 머신러닝 - 10. 교차검증(Cross Validation)과 혼동행렬(Confusion Matrix) (0) | 2019.08.13 |
| 머신러닝 - 8. Feature Scaling & Feature Selection (0) | 2019.08.04 |
| 머신러닝 - 7. K-평균 클러스터링(K-means Clustering) (4) | 2019.07.29 |
| 머신러닝 - 6. K-최근접 이웃(KNN) (6) | 2019.07.27 |




