귀퉁이 서재
[리샬 허반스] 인공지능 알고리즘 (feat. 유전 알고리즘) 본문

검색 알고리즘, 진화(유전) 알고리즘, 군집 알고리즘, 머신러닝, 딥러닝, 강화학습을 다룬 책이다.
유전 알고리즘, 군집 알고리즘, 딥러닝, 강화학습 모두 생명체에 영감을 받아 고안한 알고리즘이다. 유전 알고리즘은 진화 현상에서, 군집 알고리즘은 개미의 군집 현상에서, 딥러닝은 뉴런에서, 강화학습은 사람이나 동물의 행동(구체적으로 행동 심리학)에서 영감을 받았다. 이 책은 개념 설명에만 그치지 않는다. 알고리즘 원리를 생명 현상에 빗대어 설명한다. 그래서 이해하기가 쉽다. 이 게시글에서는 유전 알고리즘까지 정리해봤다.
Ch 1. 인공지능이란 무엇인가?
인공지능이란 무엇인지 한마디로 정의하기가 어렵다. 인공지능이 무엇인지 정의하려면 먼저 '지능'이 무엇인지 알아야 한다. 인공지능(Artificial intelligence)은 말 그대로 '인공의 지능'이기 때문이다. 그런데 문제는 지능이 무엇인지도 명확하지 않다. 살바도르 달리는 야망이 지능의 한 속성이라고 믿었다. 알버트 아인슈타인은 상상력이야말로 지능에서 가장 중요한 요소라고 보았다. 스티븐 호킹은 '지능은 변화에 적응하는 능력이다'라고 말했다. 이처럼 전문가마다 지능에 관한 의견이 다르다.

지능도 명확히 정의하지 못했으니 인공지능도 정의하기 힘들다. 이 책에서는 인공지능을 '지능적인' 행동을 하는 합성 시스템이라고 느슨하게 정의했다. '지능적'이란 무슨 뜻일까? 지능적인 사물은 일반적으로 자율적(autonomous)이고 적응적(adaptive)인 사물을 일컫는다. 여기서 자율적이라는 말은 계속 지시하지 않아도 스스로 행동한다는 의미고, 적응적이라는 말은 환경이 변하면 그에 따라 행동을 바꾼다는 의미다. 다시 풀어 말하면, 인공지능은 환경 변화에 적응해 스스로 행동하는 합성 시스템이다. 물론 느슨한 정의다.
다른 의견도 있다. 더글라스 호프스태터는 인공지능을 '아직 이루어지지 않은 모든 것'이라고 말했다. 자율주행차는 아직 완성되지 않았으므로 인공지능 요소가 있다. 하지만 훗날 자율주행차가 완벽해지면 자율주행차는 그냥 자동차일 뿐이다. 더 이상 인공지능 기술의 집합체가 아니다. 일례로 예전엔 세탁기도 인공지능이라고 광고했다. 지금 우리는 세탁기를 더 이상 인공지능 신기술의 구현체라고 생각하지 않는다. 세탁기는 그냥 세탁기이다. 인공지능의 사례로 알파고나 자율주행차는 들어도 세탁기는 들지 않는 이유다.
결론적으로 인공지능은 사람마다, 산업 분야마다, 학문 분야마다 서로 다른 의미를 가질 만큼 아직 모호한 개념이다. 명확하게 합의된 정의가 없다는 말이다. 그저 지능적으로 보이도록 구현한 시스템을 인공지능이라 통칭할 뿐이다.
Ch 2. 검색 알고리즘
우리를 지능적으로 보이게 만드는 요소는 무엇일까? 여러 가지 있겠지만, 계획을 세우고 그 계획을 잘 이행하도록 최적 방법을 찾는 행동도 그중 하나다. 우리는 매사 여러 경우의 수에서 (나름) 최적 솔루션을 찾으려고 노력한다. 이런 행동은 앞으로 살펴볼 '검색'과 관련이 있다.
검색이란?
검색 알고리즘은 변하는 환경에서 계획을 수립하고 해결 방안을 찾는 데 유용하다. 검색이란 단계적으로 계획을 세우는 걸 안내하는 방법이다. 검색 문제에는 여러 가지 솔루션이 있다. 각 솔루션은 목표를 찾는 일련의 경로(단계)를 나타낸다. 어떤 솔루션은 다른 솔루션보다 더 성능이 우수하고, 어떤 솔루션은 비용이 더 적게 든다. 비용이 적게 든다는 말은 계산량이 적다는 뜻이다. 우리가 지도상에서 지점 간 최단 거리를 구해야 한다고 치자. 거리와 교통 상황에 따라 여러 경로(솔루션)가 있다. 조건에 따라 일부 경로는 다른 경로보다 더 낫다. 이때 사용하는 알고리즘이 검색 알고리즘이다.
자료구조
자료구조는 추상화된 데이터 표현 방식(유형)이다. 여러 자료구조의 예시가 있는데, 배열(array), 스택(stack), 큐(queue), 연결 리스트(linked list), 그래프(graph), 트리(tree) 등이다. 자료구조는 문제 해결에 중요한 역할은 한다. 특히 인공지능에서 주로 사용하는 자료구조는 그래프와 트리다. 그래프는 연결 관계를 갖는 몇몇 상태를 포함하는 자료구조다. 노드(node)로 데이터 상태를 표현하고, 에지(edge)로 두 상태 간 연결을 나타낸다. 트리는 계층 구조를 나타내는 자료구조다. 계층(hierachy)이란 부모와 자식 관계 정도로 이해하면 된다. 트리는 연결된 비순환 그래프라고도 볼 수 있다. 모든 노드는 다른 노드와 연결된 에지를 가지며 그래프와 다르게 순환되지 않는다. 다음 그림은 간략한 트리와 그래프 예시이다.

트리는 바로 다음에 살펴볼 검색 알고리즘의 기본 자료구조다.
맹목적 검색 알고리즘
맹목적 검색(blind search)은 말 그대로 맹목적으로 검색하는 방법이다. 정보 없는 검색(uninformed search), 가이드 없는 검색(unguided search), 무차별 대입 검색(brute-force search)이라고도 한다. 무차별 대입해서 솔루션을 찾기 때문에 계산 비용이 많이 든다.
주요 맹목적 검색 알고리즘에는 너비 우선 탐색(breadth-first search, BFC)과 깊이 우선 탐색(depth-first search, DFS)이 있다. 너비 우선 탐색은 깊게 보기 전에 넓게 보는 탐색 방법이다. 루트 노드에서 시작해 다음 깊이의 노드를 탐색하기 전에 먼저 해당 깊이에 있는 모든 노드를 먼저 탐색한다. 반면, 깊이 우선 탐색은 넓게 보기 전에 깊게 보는 탐색 방법이다. 상황에 따라 적절한 자료구조를 사용하는 게 바람직하다. 미로 빠져나가기를 예로 들면 너비 우선 탐색 방법을 쓸 수 있다. 다음은 깊이 우선 탐색과 너비 우선 탐색의 탐색 순서 차이를 보여준다.
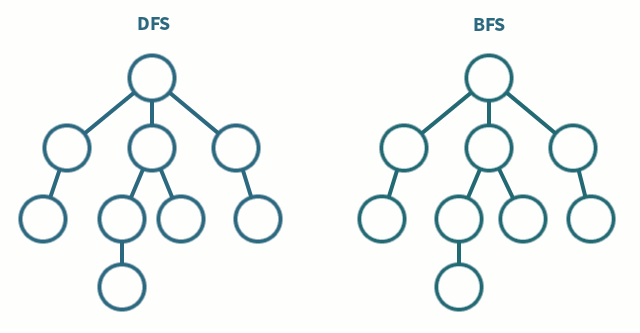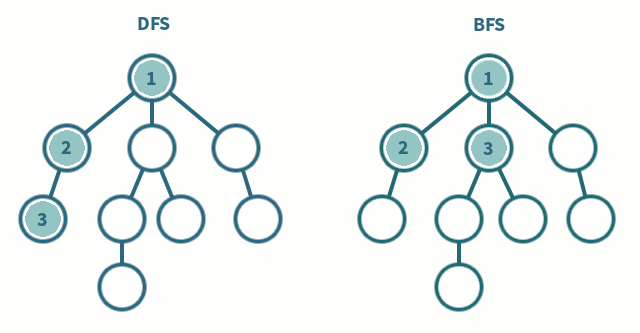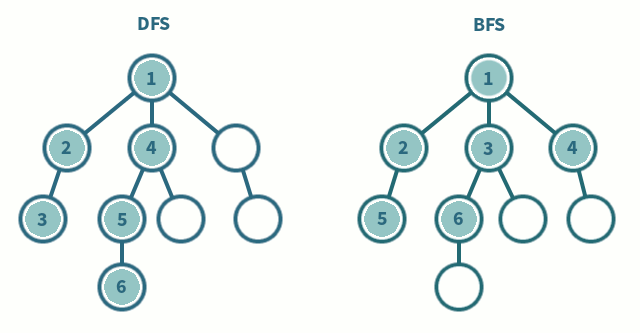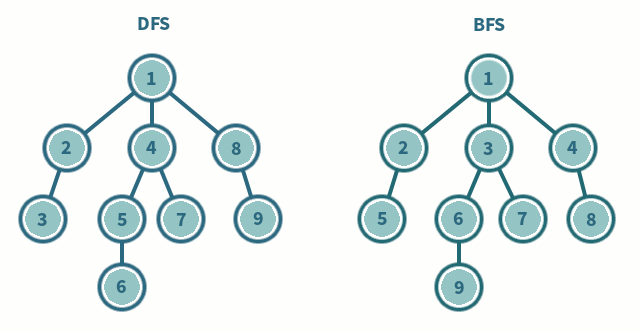
맹목적 검색 알고리즘 활용 사례
1) 네트워크 간 경로 찾기: 두 컴퓨터가 네트워크로 통신하려면 많은 컴퓨터와 장비로 연결해야 한다. 이때 검색 알고리즘을 활용해서 두 컴퓨터 간 네트워크 경로를 찾을 수 있다.
2) 웹 페이지 크롤링: 크롤러는 웹 페이지에 있는 정보를 읽고 해당 페이지에 있는 링크를 타고 다른 페이지로 이동한다. 이런 과정을 반복한다. 이때 검색 알고리즘을 사용한다.
3) SNS 친구 추천
Ch 3. 지능형 검색
지능형 검색은 Ch 2에서 다룬 맹목적 검색을 개선한 검색 방법이다. 맹목적 검색을 바탕으로, 문제에 관한 추가 정보를 활용한다. 정보에 입각한 검색(informed search), 휴리스틱 검색(heuristic search)라고도 한다. 지능형 검색은 맹목적으로 검색하지 않고, 문제에 주어진 정보를 활용해 검색한다.
예를 들어, 여행을 가는 상황을 생각해보자. 여행을 목적은 '즐거움'이다. '정해진 경비로 즐거운 여행을 다녀오자'가 목표라고 해보자. 무조건 맛있는 음식을 먹고 좋은 장소에 방문하면 목표를 달성할 수 있을까? 아니다. 경비를 생각해야 한다. 너무 돈이 많이 들면 안 된다. 맹목적 검색으로 여행 루트를 짠다면 비용을 고려하지 않을 것이다. 하지만 여행 경비가 한정된 상황이라고 가정하면, 우리는 경비도 고려해야 한다. 즉, 즐거움은 최대화하고 경비는 최소화하는 게 목적이다.
맹목적 검색을 사용해도 되는 목표 : 즐거운 여행을 다녀오자
지능형 검색을 사용해야 하는 목표 : 정해진 경비로 즐거운 여행을 다녀오자
A* 탐색
A* 탐색은 '에이 스타 탐색'이라고 말한다. A* 탐색은 특정 위치에서 목표 위치까지 가는 데 필요한 비용(cost, loss)을 최소화하는 탐색 기법이다. 무조건 최단 거리로 가는 게 목표가 아닐 때 사용한다. 가령 철수 집에서 영희 집까지 가는 상황을 생각해보자. 택시로 가면 직선거리로 빠르게 갈 수 있다. 하지만 비용이 많이 든다. 버스로 가면 뺑뺑 돌아가긴 하지만 비용이 적게 든다. 이때 수중에 돈이 버스비만큼만 있다면 버스를 타야 한다. 이처럼 특정 위치에서 목표 위치까지 가는데, 추가 제약조건이 있는 경우 A* 탐색을 사용한다.
특정 위치에서 목표 위치까지 가는 데 소요하는 비용은 다음과 같이 계산한다.
f(n) = g(n) + h(n)
- g(n): 시작 노드에서 n번 노드까지 가는 데 소요한 비용
- h(n): n번 노드에서 추가 정보를 고려해 다음 노드까지 가는 데 소요할 예상 비용
너비 우선 탐색, 깊이 우선 탐색과 같은 맹목적 탐색은 모든 경우의 수를 계산해서 최적 솔루션을 제공한다. 반면에, A* 탐색은 제약조건을 고려해 합리적인 솔루션을 제공한다.
적대적 탐색
적대적 탐색(advercarial search)이란 목표를 달성하기 위해 상대방의 행동도 예측하며 솔루션을 찾는 탐색 기법이다. 지금까지 다룬 맹목적 탐색(너비 우선 탐색, 깊이 우선 탐색)과 A* 탐색은 모두 자신의 상황만 고려했다. 맹목적 탐색은 가장 짧은 거리로 가는 솔루션을 제시하고, A* 탐색은 짧은 거리와 적은 비용을 동시에 고려해 솔루션을 제시했다. 적대적 탐색은 상대방 조건도 고려해야 한다. 바둑이나 장기, 오목과 같은 게임 상황에서 사용할 수 있다. 내 목표를 달성하기 위해 상대방 상황도 고려해야 하기 때문이다.
최소-최대 탐색
최소-최대 탐색(min-max search)은 상대에게 유리한 경로를 피하면서 본인에게 유리한 경로를 만들도록 탐색하는 기법이다. 오목을 예로 들어보자. 내가 어디에 돌을 두는지에 따라 상대방 행동이 달라진다. 그럼 상대방의 모든 행동을 기반으로 다시 내 행동을 결정한다. 이렇게 계속 반복한다. 이런 모든 경우의 수를 시뮬레이션해보고 본인이 승리할 확률이 가장 높은 곳에 돌을 두는 것이다. 메모리 제한으로 전체 경우의 수를 모두 고려할 순 없다. 지정한 횟수까지만 탐색을 한다. 최소-최대 탐색도 트리로 구현하는데, 특정 깊이까지만 탐색하는 것이다. 이게 바로 최소-최대 탐색법이다.
최소-최대 탐색은 가능한 결과를 모두 시뮬레이션하기 때문에 선택폭이 큰 게임에서 사용하기에는 계산하는 데 시간이 너무 걸린다는 단점이 있다.
알파-베타 가지치기
알파-베타 가지치기(alpha-beta pruning)는 최소-최대 탐색 알고리즘과 함께 사용하는 탐색 기법으로, 나쁜 솔루션을 생성하는(바람직하지 않은) 경로는 건너뛰어서 탐색 영역을 줄인다. 그 이유로 가지치기라고 한다. 중요하지 않은 경로는 무시하며(가지치기하며) 탐색하기 때문이다. 기본적으로 최소-최대 탐색 알고리즘으로 경로를 탐색하는데, 중요하지 않은 경로는 무시하며 진행하는 것이다.
본인의 점수는 최대화하고, 상대방의 점수는 최소화해야 한다. 최대화하려는 본인의 점수를 알파(alpha), 최소화하려는 상대방 점수를 베타(beta)라고 정한다. 때문에 이 탐색 기법 이름이 알파-베타 가지치기다. 최소화하려는 상대방의 최고점이 최대화하려는 본인의 최고점보다 낮으면, 해당 경로는 무시하고 지나간다. 이런 식으로 트리를 가지치기하며 탐색한다.
Ch 4. 진화 알고리즘
진화란 무엇인가?
진화론은 우리 모습이 어느날 갑자기 만들어진 게 아니라, 수백만 년 동안 미세한 변화를 겪으며 각 세대가 환경에 적응하면서 진화해 온 결과라는 이론이다.
찰스 다윈은 자연 선택을 중심으로 진화론을 제안했다. 자연 선택은 환경에 더 잘 적응하는 강한 개체가 살아남는다는 개념이다. 환경에 적응하지 못하는 약한 개체는 도태되지만, 강한 개체는 더 많이 번식한다. 번식 과정에서 간혹 돌연변이가 발생하기도 한다. 돌연변이가 환경에 더 잘 적응할 수도 있다. 그러면 돌연변이 형질이 더 많아지게 된다. 세대를 거듭하면서 주변 환경에 더 잘 적응하는 개체가 생존할 가능성이 커진다. 적자생존이다.
진화론에서 사용하는 용어를 정리해보자.
- 다양성: 모집단 개체는 유전적 특성이 다르다.
- 유전성: 자식은 부모에게서 유전적 특성을 물려받는다.
- 선택: 강한 개체가 생존할 가능성이 높다(적자 생존). 개체의 적합성을 측정하는 메커니즘이다.
- 번식: 모집단의 두 개체가 번식하여 자식을 낳는다.
- 교차, 돌연변이: 번식해서 낳은 자식의 유전자에는 부모의 유전자가 혼합되어 있다(교차). 간혹 유전자는 무작위로 바뀌기도 한다(돌연변이).
진화는 놀랍고도 혼란스러운 시스템이다. 세대를 거듭할수록 약한 개체는 사라지고, 강한 개체는 살아남는다. 이런 과정에서 생물은 진화한다. 진화 알고리즘은 진화 메커니즘에서 영감을 받아 만든 알고리즘이다. 생물은 진화를 통해 강해진다. 마찬가지로 진화 알고리즘은 최적 솔루션을 찾아준다. 진화의 방식으로 말이다.
진화 알고리즘을 적용할 수 있는 문제
모든 문제에 진화 알고리즘을 사용할 수 있는 건 아니다. 그러나 솔루션이 순열이나 선택으로 이루어진 최적화 문제를 해결하는 데에는 강력하다.
배낭 문제를 떠올려보자. 무게와 가격이 다른 여러 물건이 있다. 이 물건들을 배낭에 담을 수 있는데, 담은 물건의 총무게가 15kg를 넘으면 안 된다. 이때 배낭에 담은 물건의 가격이 최대가 되도록 하려면 어떤 물건들을 담아야 할까?

물건은 총 다섯 가지다. 이때 가능한 경우의 수는 2^5=32가지다. 32가지 경우의 수를 모두 고려해 각각 가격을 계산할 수 있다. 아래 표는 몇 가지 조합 예시다. 이진 인코딩 형태로 표현했다. 1이면 해당 물건을 가방에 담는다는 뜻이고, 0이면 담지 않는다는 뜻이다.
| 4$, 12kg | $2, 2kg | $2, 1kg | $1, 1kg | $10, 4kg | |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 1 | 0 | 1 | 1 |
| 3 | 0 | 1 | 1 | 1 | 1 |
| 4 | 1 | 1 | 0 | 1 | 0 |
이런 방식으로 총 32가지 조합을 만들 수 있다. 이중 총 무게가 15kg를 넘는 경우는 제외해야 한다. 이 가운데 가격이 최대가 되는 물건 조합을 구하면 된다. 경우의 수가 32가지 밖에 안 돼서 손으로도 계산할 수 있다. 하지만 항목이 많아지면 경우의 수는 기하급수적으로 늘어난다. 컴퓨터로 계산하기에도 시간이 오래 걸릴 수 있다.
이때 진화 알고리즘을 사용할 수 있다. 물론 진화 알고리즘은 최적의 솔루션을 제공하진 않는다. 최적 솔루션을 찾으려고 시도는 하지만 보장하진 못한다. 다만 주어진 조건에서 적합한 솔루션을 찾아준다. 적합한 솔루션의 기준은 문제 상황에 따라 다르겠지만 말이다. 가령 의료 시스템에서는 '충분히 좋은' 솔루션을 허용할 수 없다. 유일한 최적 솔루션을 찾아야 한다. 하지만 노래 추천 시스템이라면 '충분히 좋은' 솔루션을 허용할 수 있다. 유일한 최적 솔루션을 찾기 위해 모든 경우의 수를 고려할 필요가 없다는 말이다.
진화 알고리즘은 순열이나 선택으로 이루어진 문제에 적합하다고 했다. 물류 회사가 여러 목적지 사이 최단 경로를 찾는 경우, 공장 컨베이어 벨트에서 원재료를 가공할 때 원재료 가공 순서를 정하는 경우 등에서 사용할 수 있다. 진화 알고리즘은 그 순서를 결정하는 데 유용하기 때문이다.
유전 알고리즘
유전 알고리즘(genetic algorithm)은 진화 알고리즘에 속하는 알고리즘이다. 유전 알고리즘은 진화 메커니즘을 표방해 작동하지만, 알고리즘 수명 주기를 일부 수정해 다양한 문제를 해결한다. 유전 알고리즘은 유전체의 넓은 영역을 탐색한다. 유전 알고리즘이 항상 최적 솔루션을 찾아준다는 보장은 없다. 다만, 전체 영역에서 최적 솔루션을 찾으려고 노력한다. 최대한 지역 최솟값에 빠지지 않도록 넓은 공간을 탐색한다.
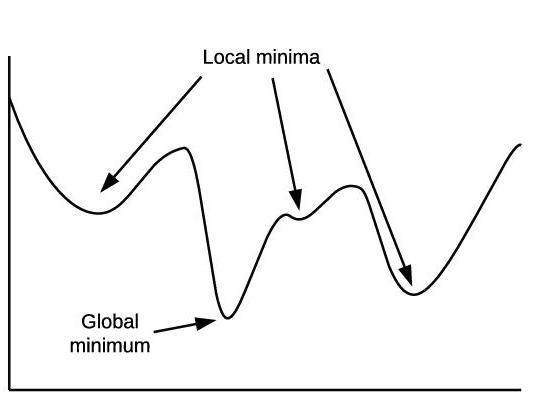
큰 검색 공간을 탐색해 지역 최솟값(local minimum)을 점진적으로 찾아내면서 결과적으로 전역 최솟값(global minimum)을 찾는다. 참고로, 목표가 최솟값을 찾는 것인지 최댓값을 찾는 것인지는 문제에 따라 달라진다.
유전 알고리즘은 각 세대가 점차 더 나은 솔루션을 찾도록 한다. 처음에는 개별 유전자 속성이 크게 달라야 한다. 그렇지 않으면 지역 최솟값에 빠질 위험이 있다. 유전 알고리즘의 수명 주기는 다음과 같다.
- 잠재적 솔루션 모집단 생성: 무작위로 잠재적 솔루션의 모집단을 만든다.
- 모집단 내 개체 적합도 평가: 잠재 솔루션이 얼마나 좋은지 평가한다. 이 작업은 적합도 함수를 활용해 계산하는데, 해당 잠재 솔루션이 얼마나 적합한지 결정한다.
- 적합도에 따른 부모 선택: 적합도 평가 결과를 기반으로 자손을 낳은 부모 쌍을 선택한다.
- 자손 번식: 선택된 부모 쌍은 자손을 낳는다. 부모 쌍의 유전 정보를 혼합(교차)하고, 약간의 돌연변이를 적용한다.
- 개체 선택: 다음 세대까지 생존할 개체를 선택한다.
- 중지: 원하는 목표에 도달했으면 유전 알고리즘을 중지한다.
한 단계씩 살펴보자.
단계 1. 잠재적 솔루션 모집단 생성
초기 모집단을 생성하는 단계다. 모집단을 초기화하는 과정에서 잠재 솔루션을 무작위로 생성한다. 문제에 제약 조건이 있다면, 제약 조건을 위반한 잠재 솔루션에는 최저 적합도 점수를 부여한다. 배낭 문제를 다시 떠올려보자. 총 32가지 경우의 수가 있다. 이중 무작위로 몇 가지만 선택해서 초기 모집단을 생성하는 것이다. 만약 총무게가 15kg를 넘는다면 적합도 평가 점수를 최저, 즉 0점을 할당한다. 다시 말하자면, 배낭 문제는 경우의 수가 32가지이지만 조합이 복잡해지면 경우의 수가 엄청나게 많아진다. 그러면 모든 경우의 수를 다 따져볼 수 없어서 몇 가지 경우의 수만 선택해야 한다. 이렇듯 단계 1은 몇 가지 초기 모집단을 생성하는 단계다.
단계 2. 모집단 내 개체 적합도 평가
단계 1에서 몇 가지 잠재 솔루션을 생성했다. 단계 2는 이 잠재 솔루션들의 적합도를 평가하는 단계다. 문제에 따라 적합도 함수를 최대화하거나 최소화해야 한다. 배낭 문제에서는 배낭에 담은 물건의 가격을 최대화하는 게 목표다. 15kg을 넘지 않는 선에서 말이다. 그러면 적합도 함수는 '물건 가격의 합'이다. 배낭 문제에서는 적합도 함수를 최대화해야 한다. 단, 물건 무게가 15kg을 넘으면 적합도 함수는 0이다.
단계 3. 적합도에 따른 부모 선택
다음 단계는 적합도에 따라 부모를 선택하는 단계다. 새로운 자식을 낳을 부모를 선택하는 것이다. 진화론에 따르면 환경에 더 잘 적응하는 개체가 일반적으로 더 오래 산다. 그런 개체가 낳은 자식들도 부모의 형질을 물려받기 때문에 환경에 잘 적응할 수 있다.
단계 2에서 구한 적합도 점수를 기반으로 새로운 자식을 낳은 부모를 선택한다. 이때 확률에 기반해 선택한다. 룰렛 휠 선택(rolette-wheel selection)은 적합도에 따라 부모를 선택하는 데 사용하는 확률적 선택 기법이다. 적합도 점수에 비례해서 룰렛 면적을 할당한다. 적합도가 높을수록 룰렛 면적이 넓다. 다음은 룰렛 휠 선택의 예시다.
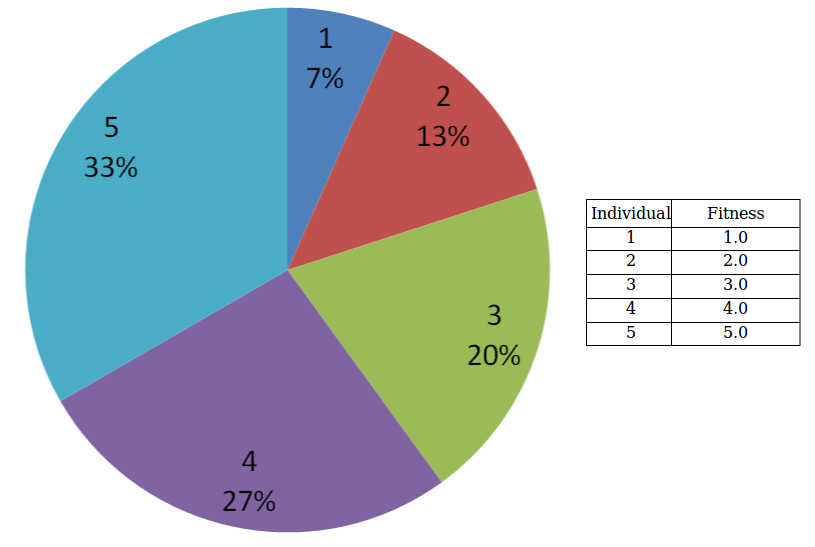
1번 솔루션의 적합도는 1이고, 5번 솔루션의 적합도는 5이다. 그렇기 때문에 5번 솔루션은 1번 솔루션에 비해 룰렛에서 5배가량 넓은 면적을 차지한다. 룰렛을 돌려 확률적으로 부모를 선택한다. 이런 속성 때문에 유전 알고리즘은 확률적이다.
자손 번식을 위해 선택한 부모 수는 필요한 총 자손 수에 따라 달라진다. 각 세대에서 원하는 개체 수에 따라 달라지는 것이다. 부모 개체를 두 개 선택해서 자손을 번식한다. 이 과정은 원하는 자손 수에 도달할 때까지 반복한다.
부모를 선택하는 방법은 룰렛 휠 선택말고도 여러 가지가 있다. 예를 들어, 순위 선택, 토너먼트 선택, 엘리트주의 선택 등이 있다. 순위 선택은 적합도 순위에 따라 휠의 면적을 배분하는 방식이다. 룰렛 휠 선택은 적합도 점수에 비례하게 면적을 배분하지만, 순위 선택은 적합도의 값보다는 순위에 따라 배분한다. 값의 크기가 중요한 게 아니라 순서가 중요한 것이다. 토너먼트 선택은 개체를 그룹으로 묶어 그룹에서 적합도가 가장 높은 개체만 선택하는 방법이다. 엘리트주의 선택은 전체 개체 중 적합도가 가장 높은 개체만 선택하는 방법이다. 엘리트주의 선택은 다양성이 떨어져 지역 최솟값(최댓값)에 빠질 우려가 있다.
단계 4. 자손 번식
부모를 선택했으니 이제 자손을 번식할 차례다. 부모가 자손을 번식하는 데에는 두 가지 방법이 있다. 첫 번째 방법은 교차(crossover)다. 교차는 아버지의 염색체와 어머니의 염색체를 일부 섞는 번식 방법이다. 부모 염색체가 혼합돼 자손이 탄생한다.
배낭 문제를 다시 떠올려보자. 앞서 살펴본 배낭 문제 조합표에서 첫 번째 조합과 두 번째 조합은 각각 [10110]과 [01011]이다. 두 조합을 부모의 염색체라고 해보자. 교차 방법으로 자손을 번식하면 이렇다.
부부: 1 0 1 1 0
모모: 0 1 0 1 1
자손: 1 0 0 1 1
앞의 두 염색체는 아버지(부) 것을 물려 받았다(1 0). 뒤의 세 염색체는 어머지(모) 것을 물려받았다(0 1 1). 이런 방식으로 교차가 이루어진다. 이 교차 방법은 하나의 예시일 뿐이다. 다른 교차 방법으로도 번식이 가능하다.
두 번째 방법은 돌연변이(mutation)다. 돌연변이는 염색체를 무작위로 변경하는 번식 방법이다. 여기서 염색체라고 표현했지만 배낭 문제를 떠올리면 물건 조합이라고 생각하면 된다. 돌연변이는 개체를 다양하게 변화시켜준다. 개체 다양성을 강화하고 알고리즘이 지역 최솟값(최댓값)에 갇히지 않도록 한다. 하지만 너무 많은 돌연변이는 오히려 솔루션의 적합도를 떨어뜨릴 수 있다. 뭐든지 적당한 게 좋지 않은가?
단계 5. 개체 선택
자손을 번식했으니 다음 세대에 생존할 개체를 선택해야 한다. 일반적으로 모집단 크기는 고정되어 있다. 각 세대별로 생존하는 개체 수는 일정하다는 말이다. 부모가 번식해서 자손을 낳았으니 유입된 개체만큼 일부 개체는 제거해야 한다. 어떻게 살아남을 개체를 선택해야 할까? 무조건 우수한 개체를 살아 남기는 게 좋아 보이지만 항상 그렇진 않다. 생존한 개체의 유전적 특성이 비슷하다면 다양성이 떨어진다. 다양성이 떨어진다는 말은 지역 최솟값(최댓값)에 갇힌다는 말이다. 그래서 우수한 개체를 선택하되 다양성도 같이 고려해주어야 한다. 이를 탐험(exploration)과 활용(exploitation)이라고 한다. 탐험은 다양성을 강화하는 방법, 활용은 우수한 개체를 선택하는 방법이다. 탐험과 활용 사이에서 균형을 맞추는 게 중요하다.
이렇게 개체를 선택했으면 다시 처음부터 반복한다. 살아 남은 개체를 토대로 적합도를 평가하고, 적합도에 따라 부모를 선택하고, 자손을 번식하고, 개체를 선택한다.
단계 6. 중지
유전 알고리즘은 중지 조건이 없으면 계속 반복한다. 물론 실제 생물은 멸종하기 전까진 진화를 멈추지 않는다. 하지만 우리는 문제를 해결해야 하기 때문에 알고리즘을 언젠간 중지해야 한다. "적합도 평가 → 부모 선택 → 자손 번식 → 개체 선택"의 반복을 언제 중지해야 할까?
가장 간단한 중지 조건은 반복 횟수를 지정하는 조건이다. 또 다른 방법은 특정 적합도에 도달하면 중단하는 방법이다. 적합도가 더 이상 좋아지지 않으면 중단하는 방법도 있다. 적합도가 정체되면 미래 세대에 더 나은 솔루션을 찾을 가능성도 줄어들기 때문이다. 머신러닝에서 사용하는 조기 종료(early stopping) 개념과 유사하다.
유전 알고리즘 매개변수 설정
지금까지 유전 알고리즘의 수명 주기를 알아봤다. 유전 알고리즘을 설계할 때 매개변수를 설정할 수 있다. 매개변수에 따라 알고리즘 성능이 결정된다.
- 모집단 크기: 모집단이 클수록 잠재 솔루션이 다양해진다. 다만 모집단이 클수록 더 많은 계산을 해야 한다.
- 자손의 수: 각 세대에서 생성할 자손의 수를 설정한다.
- 부모 선택 방법: 부모를 선택하는 방법을 설정한다. 앞서 설명했듯 탐험과 활용을 균형 있게 활용해야 한다.
- 교차 방법: 교차 방법은 다양하다. 이 교차 방법에 따라 자손의 유전자가 결정된다.
- 돌연변이 비율: 돌연변이가 많으면 더 다양한 잠재 솔루션을 만든다. 하지만 돌연변이 비율이 너무 높으면 오히려 적합도가 떨어진다. 초기에는 돌연변이 비율을 높여 다양성을 키우고, 후기에는 돌연변이 비율을 낮추어 우수한 개체를 활용하는 방법도 있다. 바꿔 말해, 초기에는 탐험 비율을 높이고, 후기에는 활용 비율을 높이는 방법이다.
- 세대 선택 방법: 남아 있는 부모 + 부모가 낳은 자식 가운데 살아남을 다음 개체를 선택해야 한다. 이때 선택한 방법에 따라 알고리즘이 빨리 수렴할 수 있고, 오래 탐험할 수도 있다.
- 중지 조건: 계산 복잡성과 시간은 중지 조건의 주된 관심사다.
지금까지 유전 알고리즘을 살펴봤다. 유전 알고리즘은 무작위성을 현명하게 이용해 우수한 솔루션을 빠르게 찾는 방법이다. 유전 알고리즘과 관련한 재밌는 유튜브 영상이 있다. 유전 알고리즘으로 그네 타는 법을 학습하는 영상이다. 꼭 한 번 보길 바란다.
이 영상에서도 세대와 유전자라는 용어가 나온다. 세대를 거듭할수록 유전자가 바뀐다. 그네를 더 잘 타는 유전자로 진화하는 것이다. 다시 말해 적합도가 높은 개체가 살아남는다. 유전 알고리즘을 중지한 세대는 22세대다. 이 지점부터는 유전자 변화가 거의 없어지기 때문이다.
'책과 사유' 카테고리의 다른 글
| [류시화 엮음] 마음챙김의 시 (0) | 2021.09.21 |
|---|---|
| [수 클리볼드] 나는 가해자의 엄마입니다 (0) | 2021.09.18 |
| [쇼펜하우어] 인생론 (2) | 2021.08.04 |
| [한강] 채식주의자 (0) | 2021.07.23 |
| [뤼디거 자프란스키] 니체 (2) | 2021.07.07 |




